Institute of Mathematical Geography

Map transformation is an idea that is familiar to most geographers (Tobler, 1961; Thompson, 1917; Coxeter, 1961). A QR code might be viewed as a "map"---it employs a mathematical code to direct understanding of content. While the geographical map uses mathematics to guide understanding of content of the Earth, the QR code map uses mathematics to guide understanding within electronic worlds (link to general pattern of meaning within a QR code).

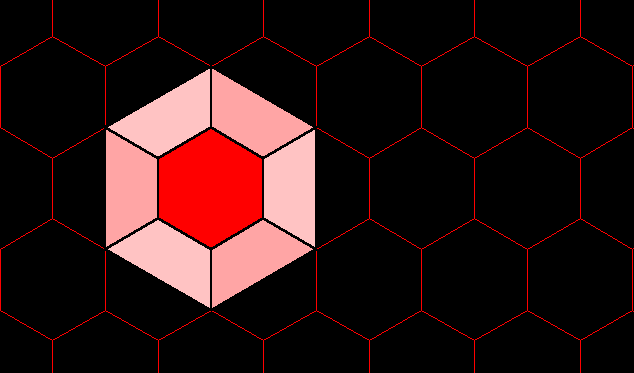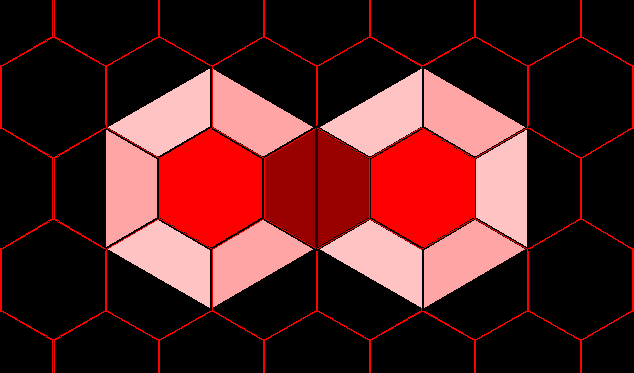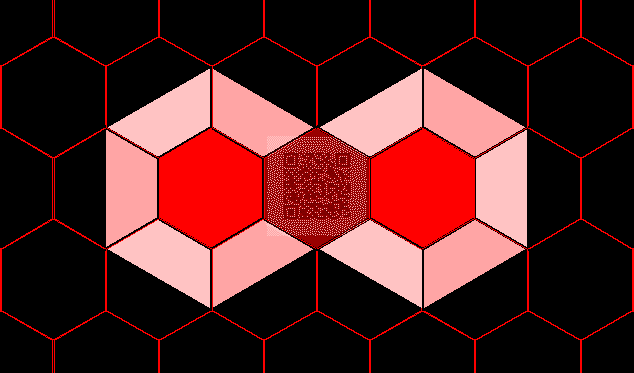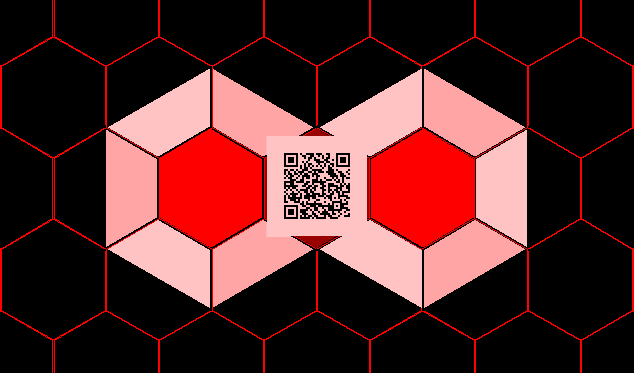
One might ask questions about QR codes in the same way one does about geographical maps. Not all regions of a map carry equal weight (land masses on one map might be more important than water masses). The same observation is true about QR codes--different regions of the image carry different weights (as indicated in material in the link above). The thoughtful reader will think of numerous parallels. Is there some sort of parallel world of QR-cartography?

Geometric Transformations

Rotation (turn), reflection (flip), and translation (slide) form a basic set of movements of figures in the plane (Coxeter, 1961). In the case of a QR code pattern in a box, it is clear that translation does not affect the code--simply slide the smartphone to catch up with the sliding motion of the QR code box. Do rotation and reflection of the surface pattern in the box alter the linkage to a website? Does the embedded link to a website get destroyed by such motion? If not, does the link remain constant under such transformation. Again, it seems clear that if the link is not destroyed that then the rotated or reflected QR code would point to the same url as the original QR code box....it is simply the surface pattern and not the embedded code that is being transformed. Figure 1 shows a single QR code that has had transformations applied to it. Figure 1a is the "original" pattern. Figure 1b shows the pattern with a horizontal flip. Figure 1c shows the pattern with a vertical flip. Figure 1d shows it rotated 45 degrees clockwise.

Figure 1a. Base QR code. Links to IMaGe home site.

Figure 1b. Horizontal flip of Figure 1a.

Figure 1c. Vertical flip of Figure 1a.

Figure 1d. Rotation of Figure 1a through 45 degrees clockwise.

This simple experiment suggests that rotation does not destroy the linkage of the pattern to a website but that reflection does do so. At first, this result might seem surprising. If, however, one returns to the analogy of QR codes and geographic maps, it might not. The difference is that QR code patterns are not sensible to our eye whereas many map patterns are. Thus, in the sequence of maps in Figures 2a through 2d, it makes sense that the original and the rotated map (Figures 2a and 2d) are equivalent in terms of content but that the flipped maps in Figures 2b and 2c are not sensible in that regard. Nonetheless, QR codes such as the flipped ones that are not sensible from an overhead view might become useful in situations where one wishes to look at the QR code from the back or from underneath. The animation in Figure 2c shows the distinction between rotating the map through 180 degrees (so that north and south are interchanged) and reflecting, or flipping, the map.

Figure 2a. Map of the world. Source: Public Domain, http://en.wikipedia.org/wiki/File:BlankMap-World-162E-flat.svg

Figure 2b. Horizontal reflection of the map in Figure 2a.

Figure 2c. Animation showing difference between a vertical reflection of the map in Figure 2a and a rotation through 180 degrees of the map in Figure 2a.

Figure 2d. Rotation through 45 degrees of the map in Figure 2a.

If one looks further, at the interleaving of data and error correcting blocks that lie behind the QR code pattern, then one sees immediately--due to lack of symmetry, that the Escher-like tiles of data are preserved under rotation but not under reflection (Figures 3a through 3d).

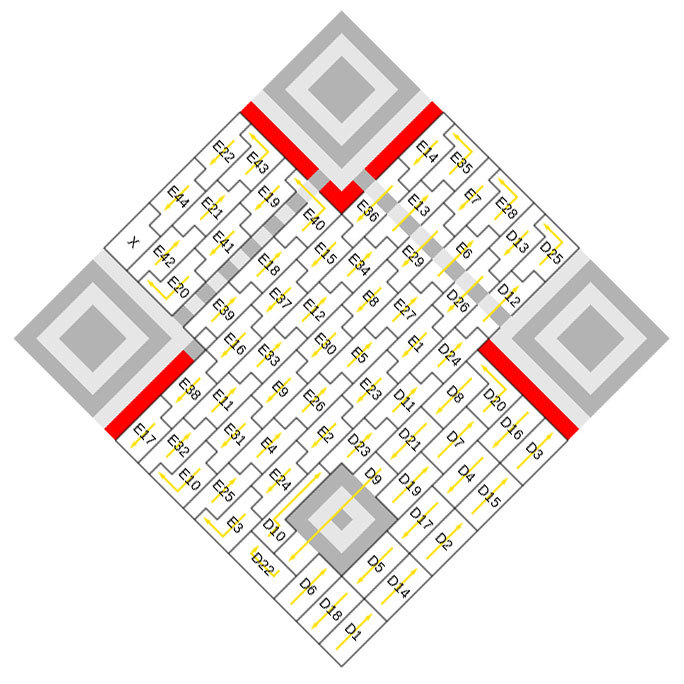Figure 3a. Interleaving of tiles of data and error correction in tiles that change position under reflection but not under rotation. Source: Public Domain, "Bobmath", Wikipedia, Jan. 9, 2012: http://en.wikipedia.org/wiki/File:QR_Ver3_Codeword_Ordering.svg
Figure 3b. Horizontal reflection alters relative interleaving of tiles.	Figure 3c. Vertical reflection alters relative interleaving of tiles.

Figure 3d. Rotation through 45 degrees does not alter relative interleaving of tiles.

Permutation Group of the Symmetries of a Square

Legal motions of a QR code form a subgroup of the group of motions of symmetries of a square. It is the subgroup of rotations. The QR code is invariant under the geometric transformations of rotation and translation, but not under reflection.