| SOLSTICE: An Electronic Journal of Geography and Mathematics Persistent
URL: http://deepblue.lib.umich.edu/handle/2027.42/58219
|
 |
Works best with a high speed internet connection.
| SOLSTICE: An Electronic Journal of Geography and Mathematics Persistent
URL: http://deepblue.lib.umich.edu/handle/2027.42/58219
|
 |
June, 2012 |
|
From
Tissot to Google Earth: Sampling the Earth's Graticule
Sandra L. Arlinghaus and Joseph Kerski Associated .kmz download.  Sampling Projection Distortion: Tissot's Indicatrix Classical
Approach: Mercator and Sinusoidal Projections
The Tissot Indicatrix, is the classical way
to sample projection
distortion. A sequence of circles of constant radius are centered
on graticule intersection points. The greater the associated
distortion in mapping the globe to the plane, the greater the
distortion of the circle, either as an enlarged circle, or as an
ellipse with long major axis in relation to its minor axis.
Figure 1 shows a typical illustration indicating this idea with simple
enlargement on a Mercator projection and Figure 2 shows circular
elongation on a sinusoidal projection.
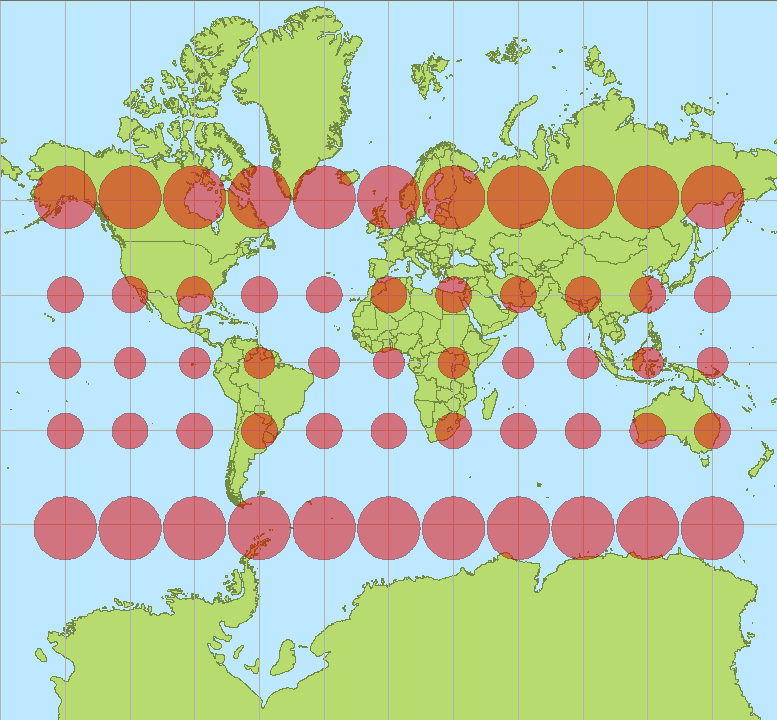 Figure 1. Tissot Indicatrix, Mercator
projection
Source: Wikipedia--http://en.wikipedia.org/wiki/File:Tissot_mercator.png 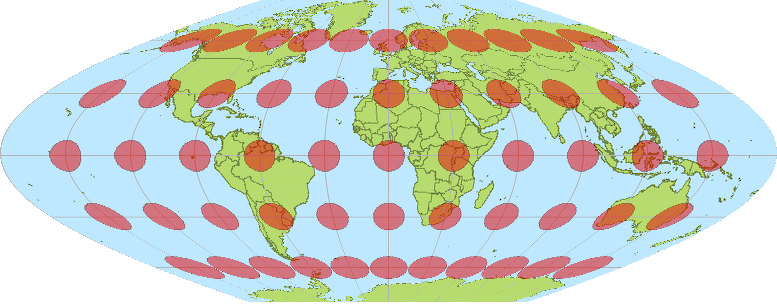 Figure
2. Tissot Indicatrix, Sinusoidal projection.
Source: Wikipedia--http://en.wikipedia.org/wiki/File:Sinusiodal_earth_circles.png Figure 1 illustrates quite clearly the way in which landmasses become exaggerated in area as one moves toward the poles while Figure 2 illustrates a change in shape, rather than in area, as one moves poleward. While the visual evidence is compelling, it is difficult to see simultaneously in the mind's eye how the graticule distortion might distort a variety of globe features. One reason for this difficulty is that these models are visually static. Indeed, usually, as in Figures 1 and 2, one sees only simple country-level boundary distortion in association with ellipse elongation. Contemporary Approach: Web Mercator
Auxiliary Sphere projection
Software in which one can traverse an image of the globe, such as Google Earth, offers a dynamic way to both see Tissot-style distortion and simultaneously consider an inventory of what is available on the globe through digital imagery. Figure 3 shows an approach to an alternative visual sampling of projection distortion; here, of the Web Mercator Auxiliary Sphere projection. 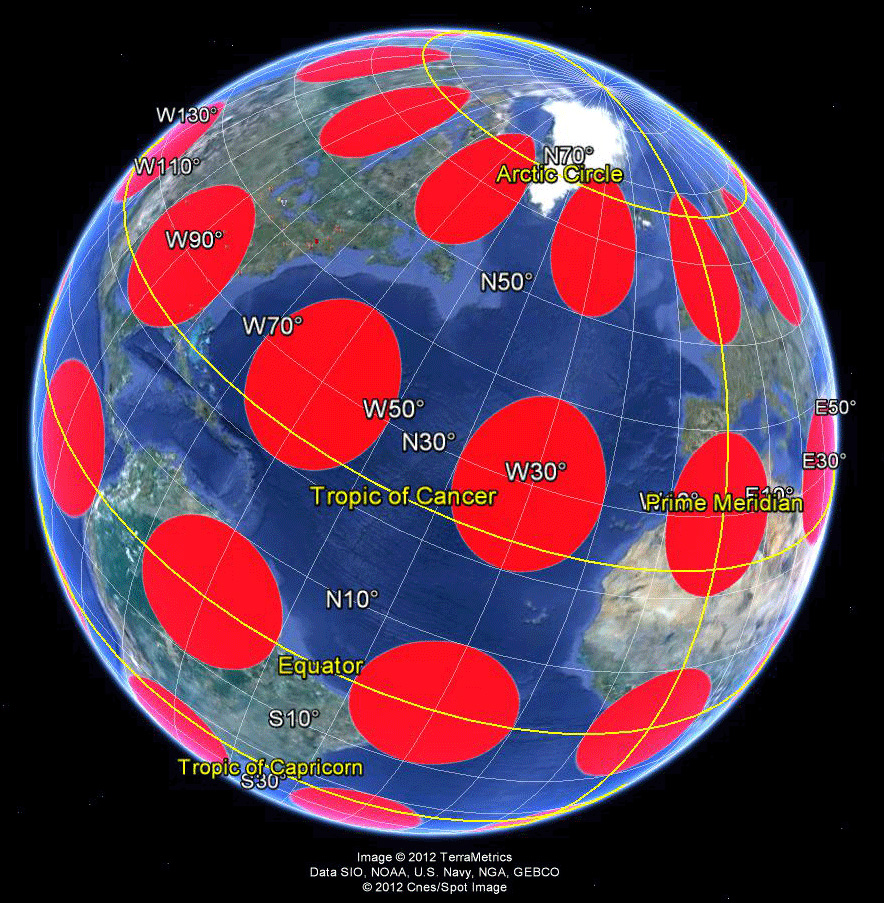 Figure 3. Tissot Indicatrix of Web Mercator Auxiliary Sphere projection with distortion realized in Google Earth. Screen captures, and animations of screen captures, show less than half the Google globe. To see it all, download the associated .kmz file and open it in Google Earth. One advantage, in addition to being able to spin the globe, is to adjust the opacity of the ellipses, the elevation of the ellipses, the scale of visualization, and a host of other factors. The following visual sequence suggests a number of different possibilities. No doubt the interested reader will find others! The animation in Figure 4 suggests that when looking at a broad region, the elongation of the ellipse might matter when looking at global patterns, such as weather fronts. The radar imagery may be stretched a bit in the north-south direction so care must be taken to interpret the pattern in relation to existing boundaries or benchmarks rather than simply on sheer apparent length of the front. The animation in Figure 5 suggests, however, that local scale studies suffer few effects from the distortion. In fact, the semi-transparent overlay of the ellipse offers no information and simply clouds the wealth of default information available in the mapping software. Figure 6 returns again to a global view and raises the ellipses above the surface of the globe so that one might walk between the globe and the Tissot layer to view simultaneously the terrain and the superimposed polygons from within the abstract structure. This Tissot umbrella offers unusual vantange points; again, the reader might try this construction, and similar ones, for him or herself using the downloaded .kmz file. This sort of approach, to integrating geometry and geography, is a small sample of what is to come in our forthcoming book on spatial mathematics...stay tuned. |
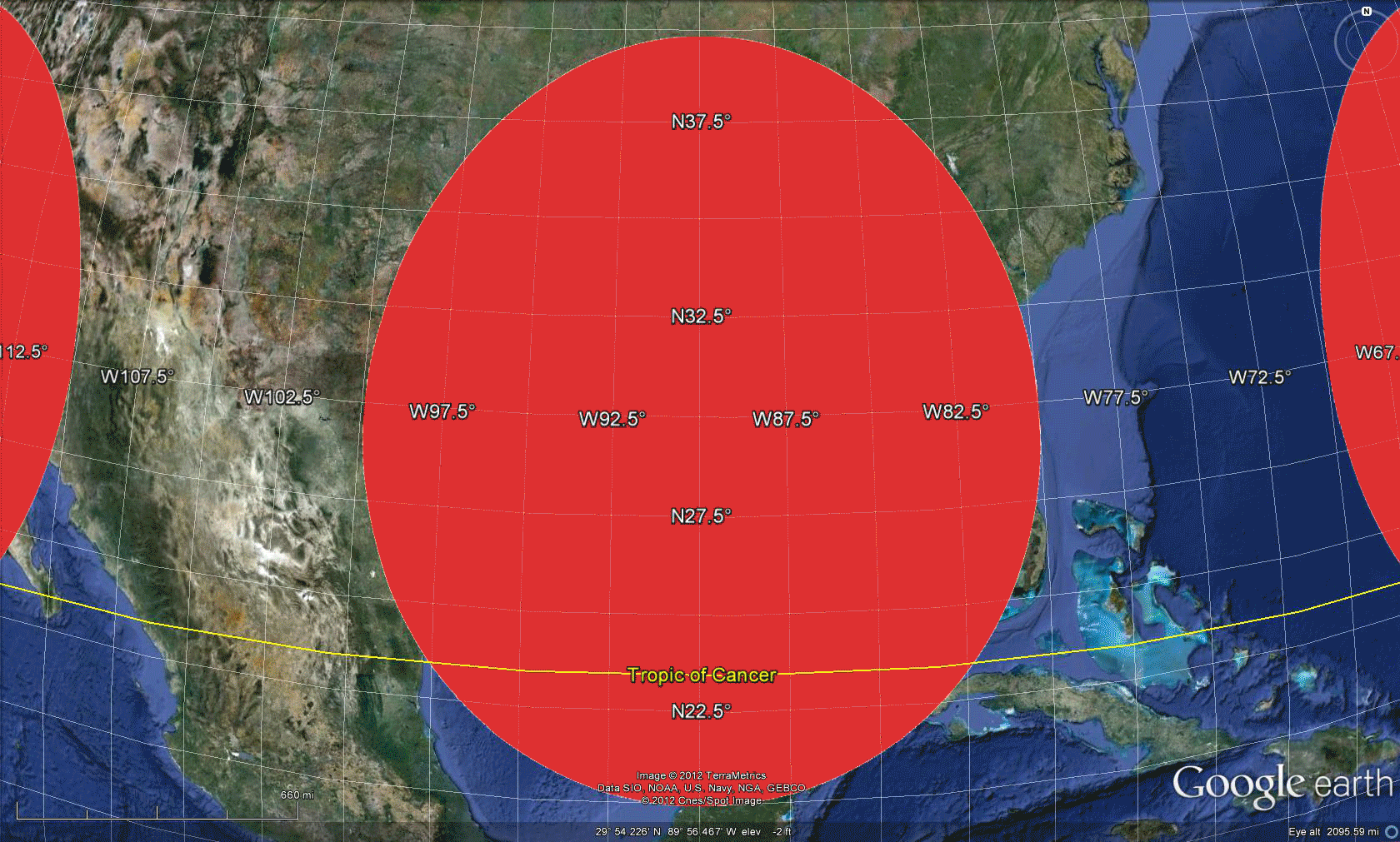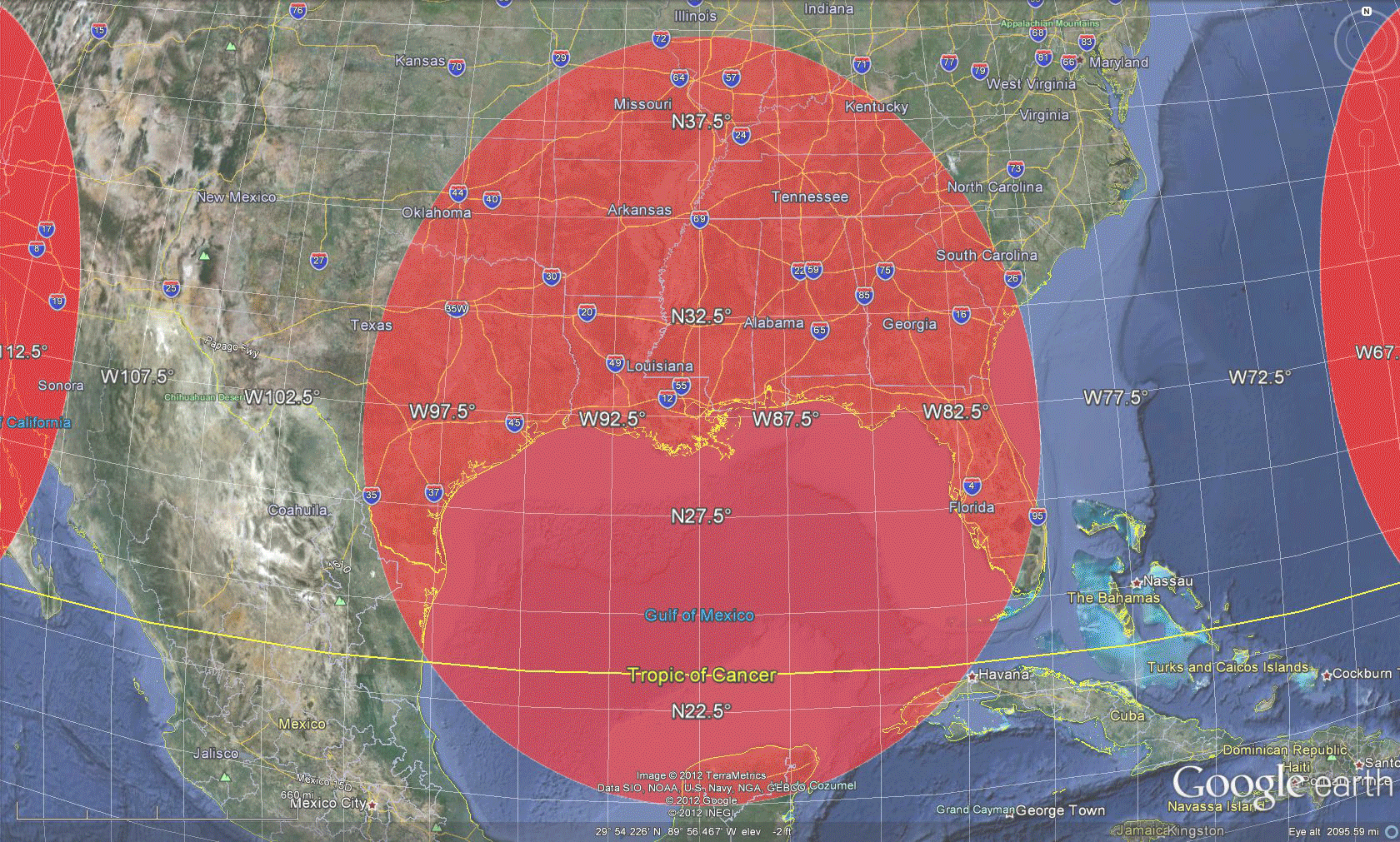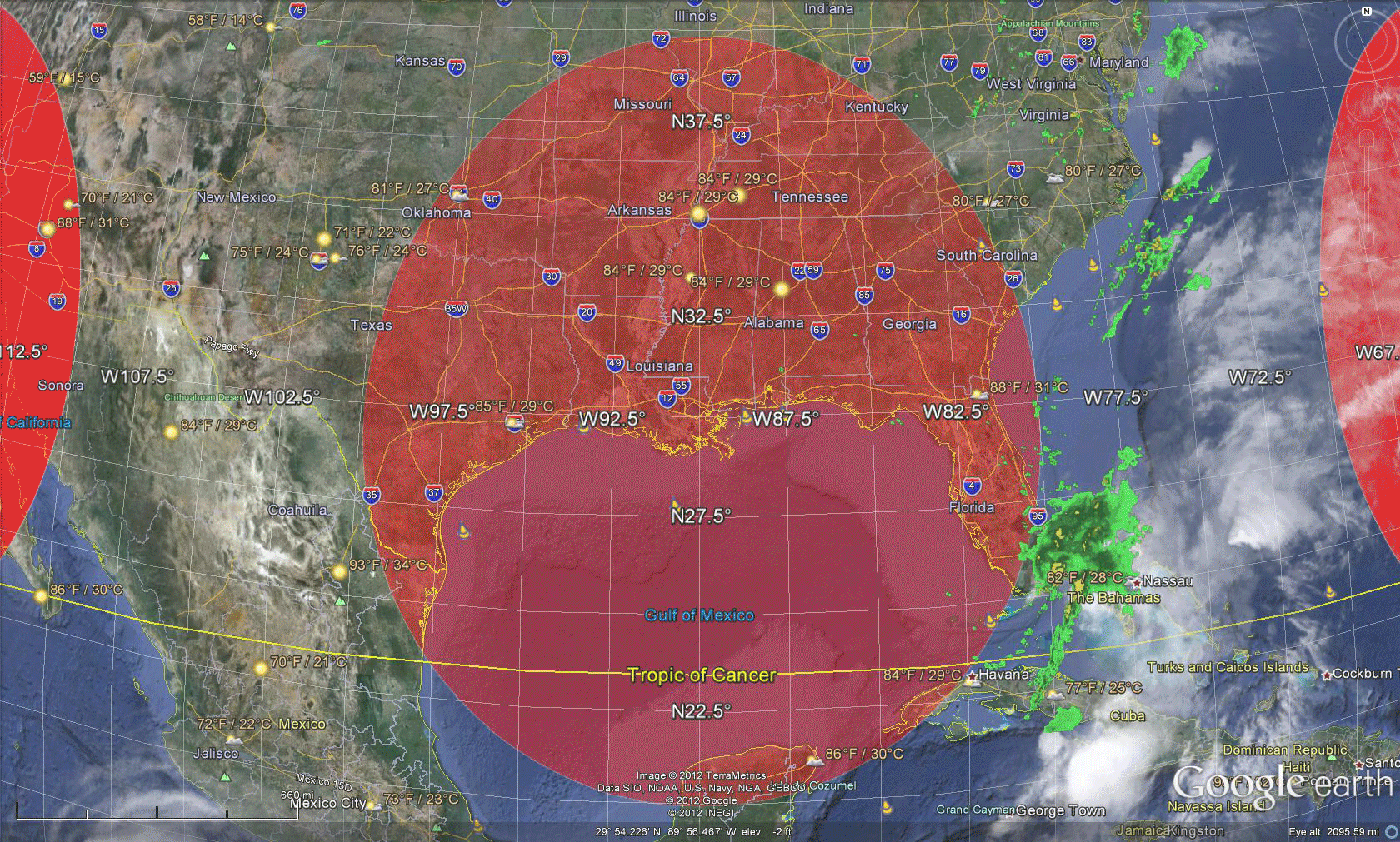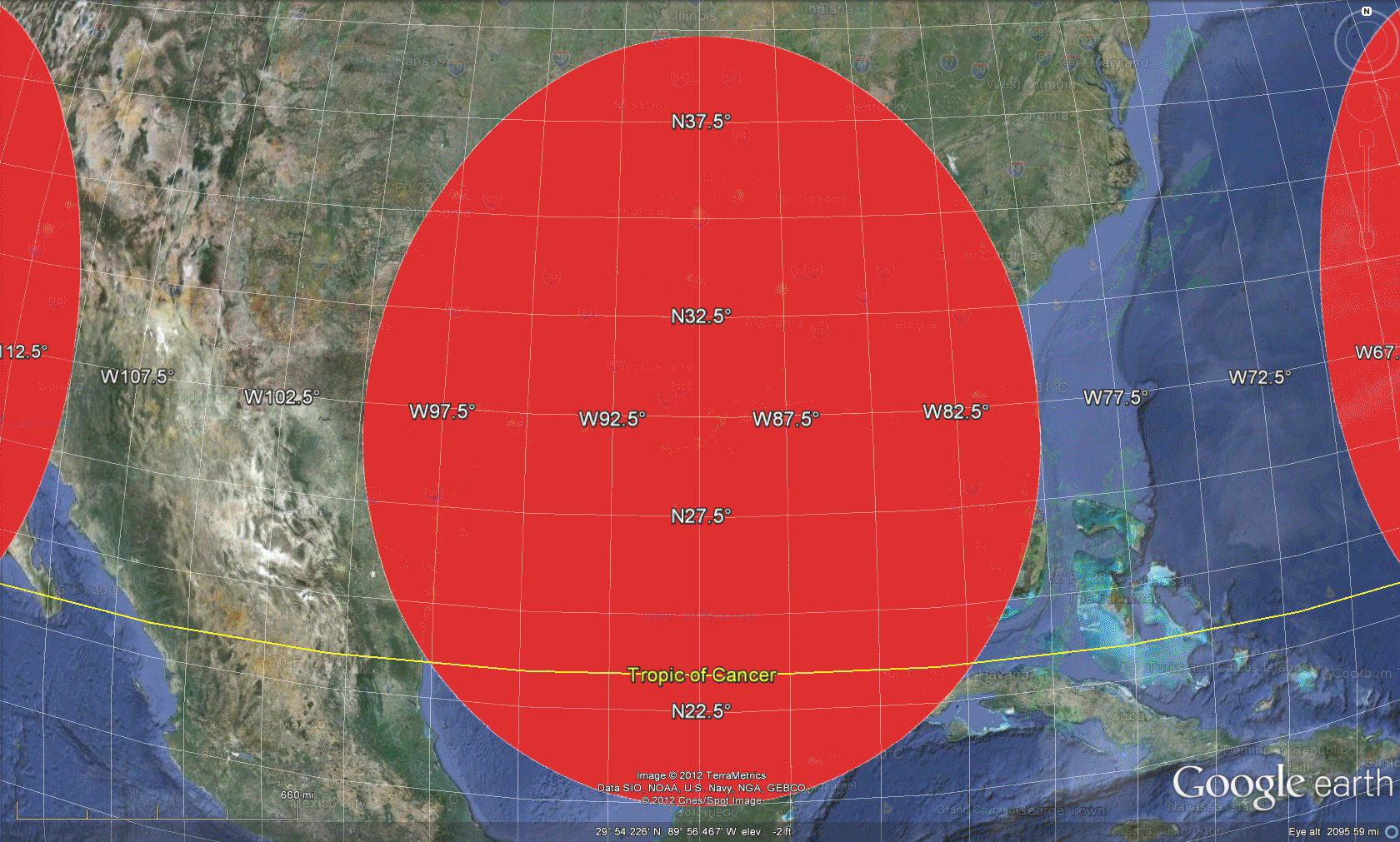
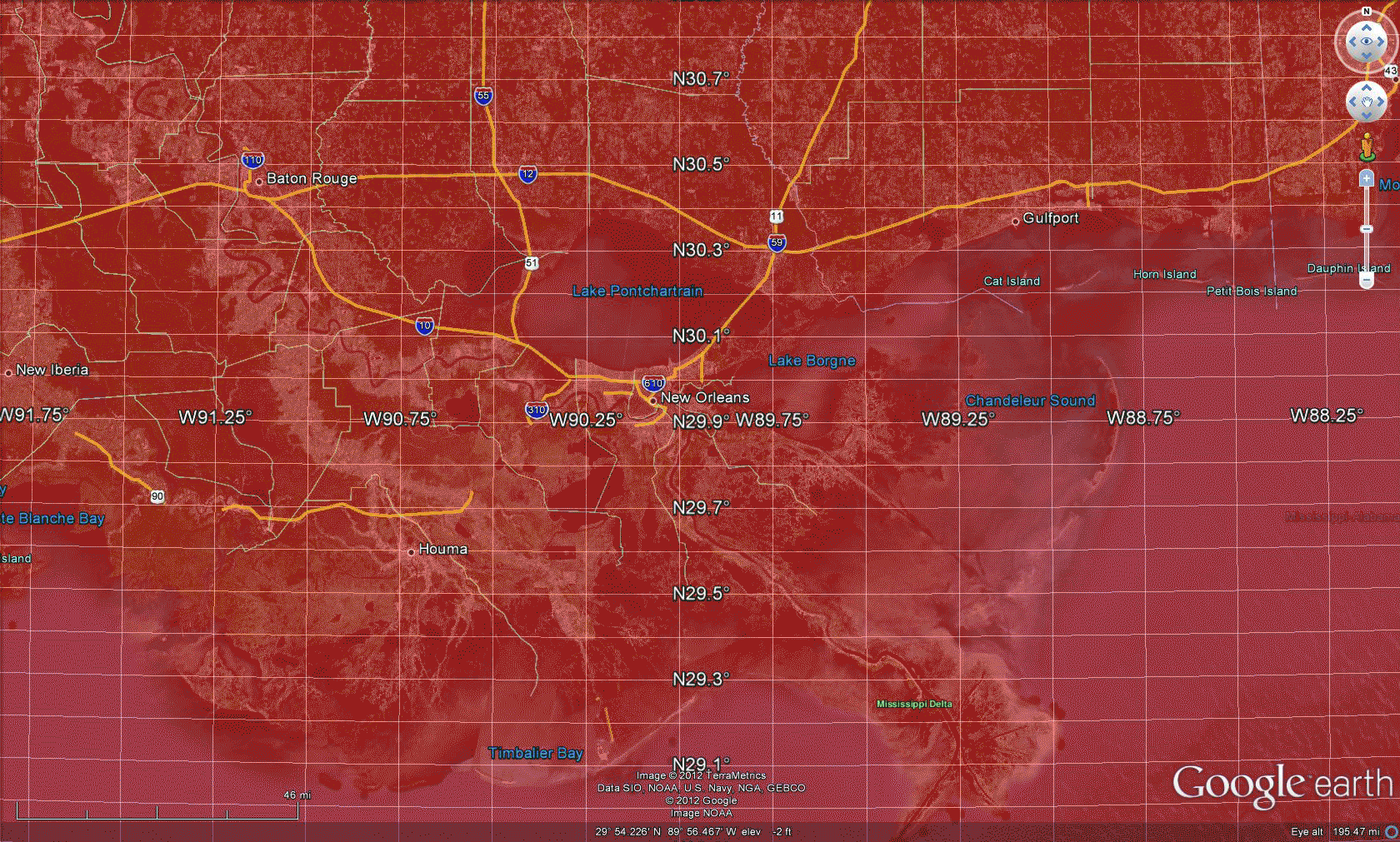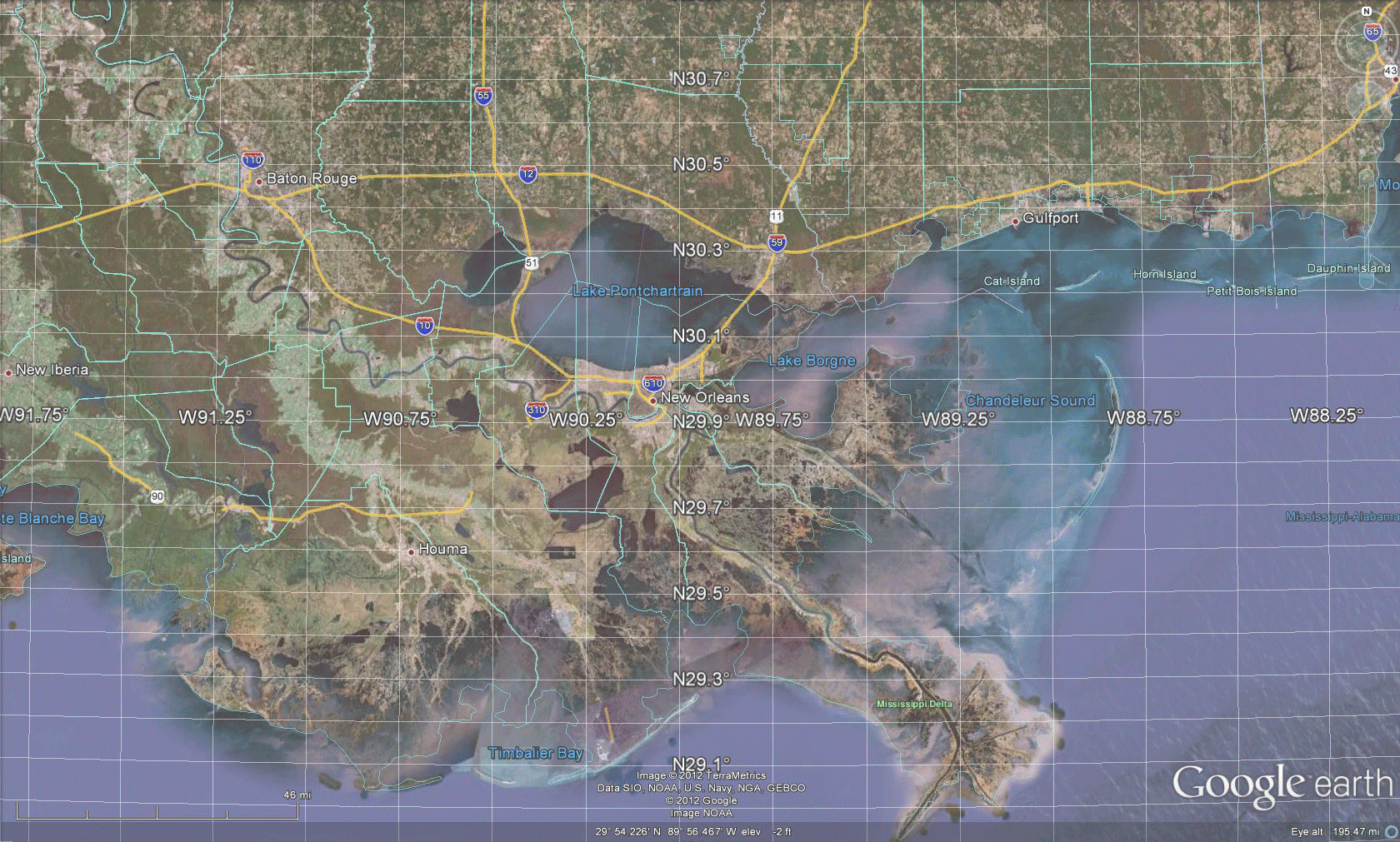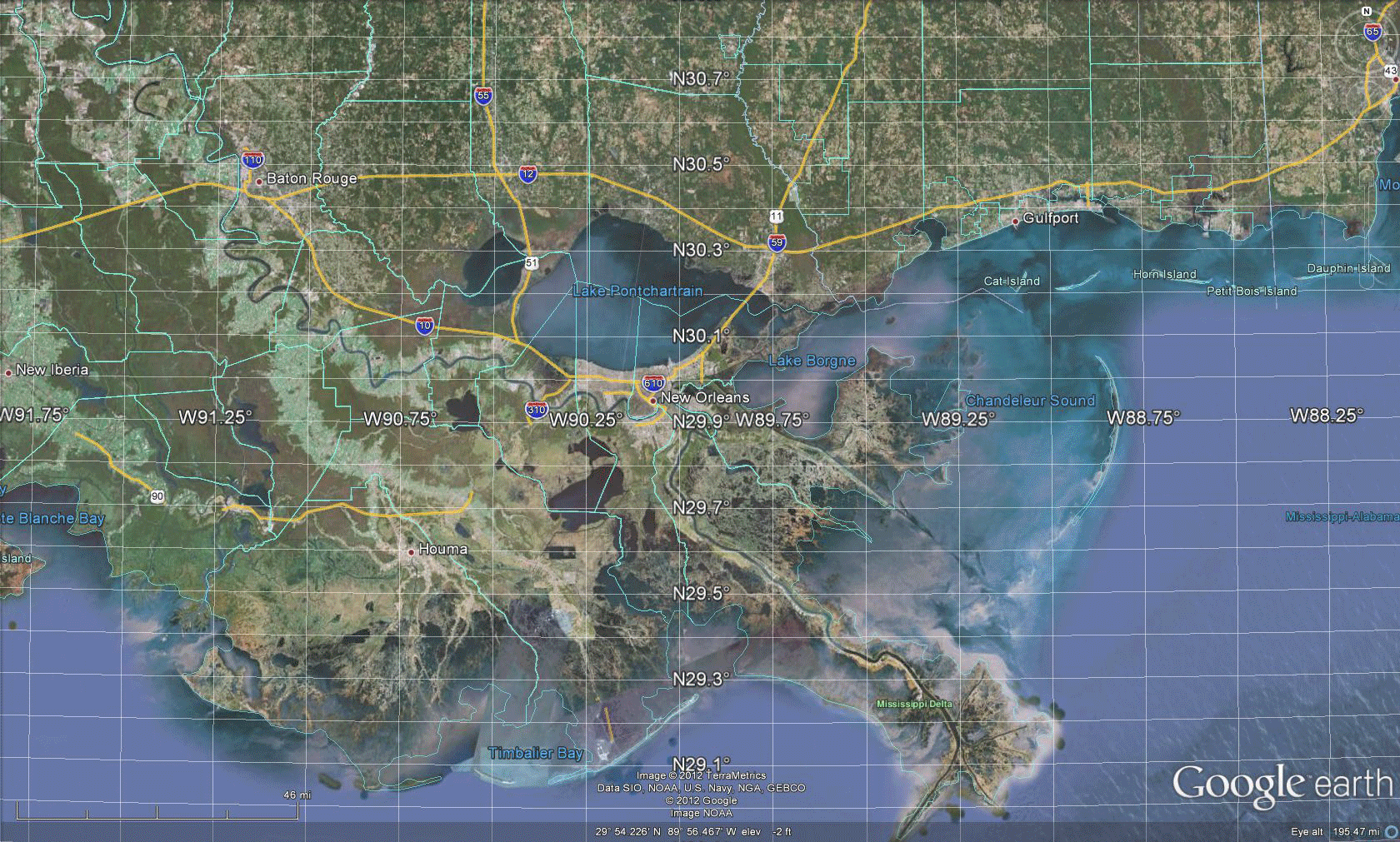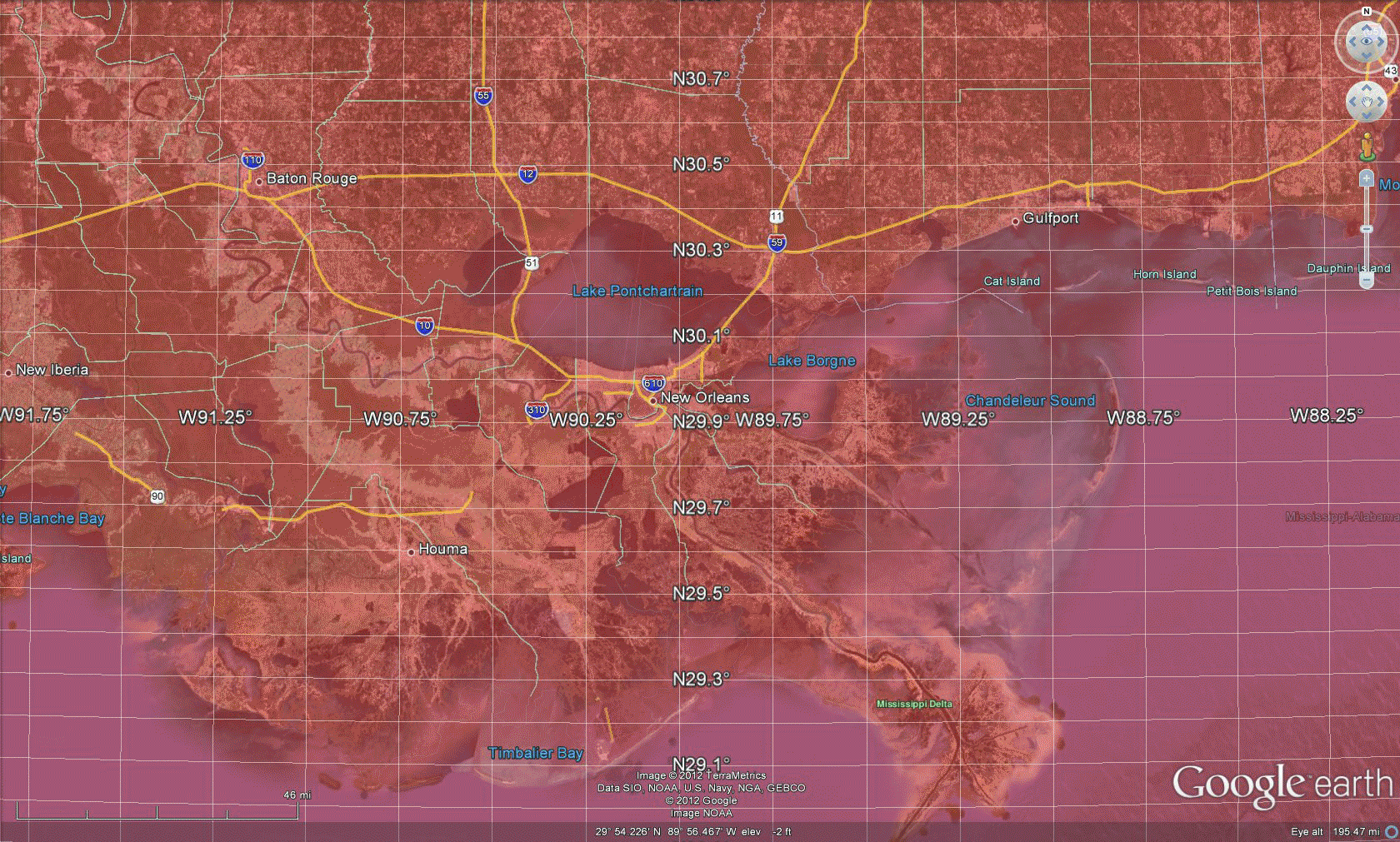

| Sampling the
Environment: the Degree Confluence Project The Tissot Indicatrix samples the graticule at the global, or at least, small scale level. A more recent project, called the Degree Confluence Project, photographically samples the Earth's graticule at integer locations of parallels and meridians in order to create an archived inventory at these locations. Try the worldwide confluence navigation tool posted on the DCP website: http://confluence.org/worldwide.php . Consider individual photos and reports of the set of discrete locations (Kerski Confluence visit at 42N, 84W, a sample typical of such visits) . Each one gives an amount of geographic information confined by latitude and longitude within a small capsule, much as postage stamps have done so in the past. Indeed, the collection digital photographs, mounted in an "album" of Google Maps is much like the archives of the journal The CartoPhilatelist that emphasizes maps on stamps and associated stories; here, the compact stories are mounted digitally and are fashioned from virtual images--as perhaps a different contemporary view of cartophilately! References Arlinghaus, S. and Kerski, J. Spatial Mathematics: Theory and Practice Through GIS. CRC Press, Forthcoming, 2012. The CartoPhilatelic Society. http://www.mapsonstamps.com/ Degree Confluence Project, http://confluence.org/ Kerski, Joseph. 2012. Confluences. Stefan Kühn. 2004. Wikipedia, Tissot's Indicatrix by Mercator-Projection. http://en.wikipedia.org/wiki/File:Tissot_mercator.png Gregory F. Maxwell. 2006. Wikipedia, A sinusiodal reprojection of Image:Tissot_mercator.png by Stefan Kühn. http://en.wikipedia.org/wiki/File:Sinusiodal_earth_circles.png Tissot's Indicatrix, Wikipedia, http://en.wikipedia.org/wiki/Tissot%27s_indicatrix |
 |
|||
| 1.
ARCHIVE 2. Editorial Board, Advice to Authors, Mission Statement 3. Awards
|
|
.

Solstice:
An Electronic Journal of Geography and Mathematics, |
|
Congratulations to all Solstice contributors. |
| Remembering
those who
are gone now but who contributed in various ways to Solstice
or to IMaGe
projects, directly or indirectly, during the first 25 years of IMaGe: Allen K. Philbrick | Donald F. Lach | Frank Harary | William D. Drake | H. S. M. Coxeter | Saunders Mac Lane | Chauncy D. Harris | Norton S. Ginsburg | Sylvia L. Thrupp | Arthur L. Loeb | George Kish | |