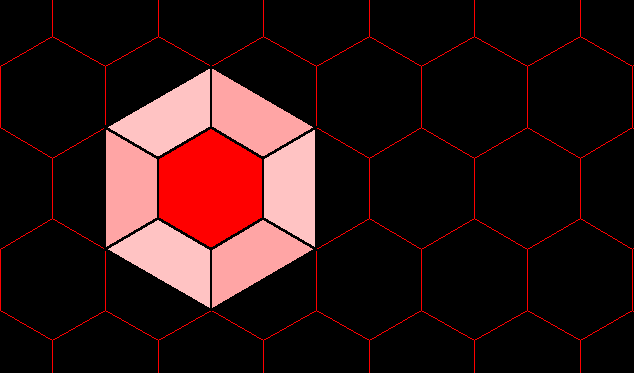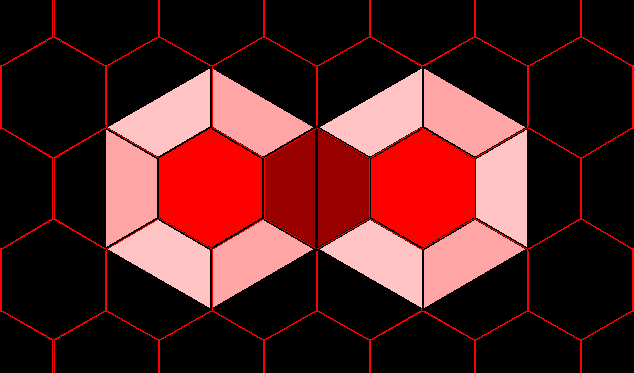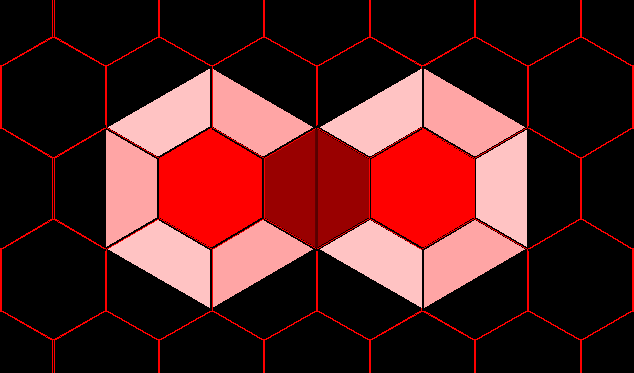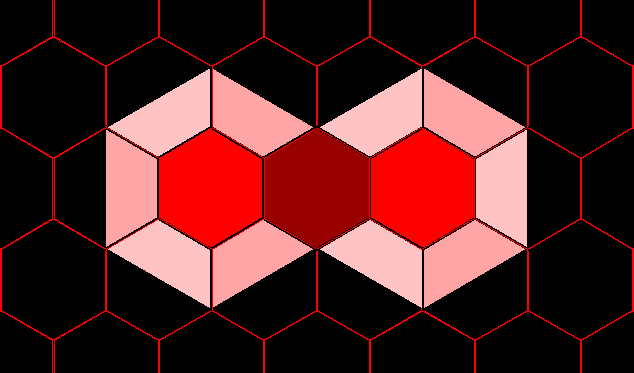
 Figure 0.1. Spatial synthesis: abstract representation. |
| The brain is wider than the
sky, For put them side by side; The one the other will include, With ease, and You beside. Emily Dickinson |
Synthesis begins with a global view and dissects that view to consider individual components, as they contribute to that whole: the whole is often more than the sum of the individual parts considered. In contrast, analysis often begins with a sequence of local views and assembles a global view from these, as a sum of parts: the assembled view may or may not fit "reality." These two different approaches to scholarship yield different results and employ different tools. In this work, we take a synthetic approach to looking at real world issues that have mathematics as a critical, but often unseen, component. This approach permits one, also, to learn the associated mathematics as it naturally unfolds in real world settings, often in a relatively "painless" manner. The reader learns mathematics required to consider the broad problem at hand, rather than learning mathematics according to the determination of a (perhaps) artificial curriculum. The underlying philosophy is different, as is the format. The eBook is required, however, given the interactive and animated features that enliven the book and motivate the reader to explore diverse realms in the worlds of geography and mathematics and in their interface.
Figure
0.1 offers an abstract view of the idea of "spatial synthesis."
Each
large hexagon represents a single scholarly discipline:
mathematics
on the left and geography on the right (as an example). A single
field (geometry, for example) is identified (deep red trapezoid) from
one
the broad discipline of mathematics, and is aligned with a counterpart
(deep red trapezoid) field (cartography) from the other broad
discipline
of geography. Despite the alignment of appropriate entities, a
gap
remains. In institutional settings reliant on predetermined
disciplinary
boundaries, interdisciplinary research often founders in this gap for
lack
of support of various kinds. What is required, therefore, is to
seal
the gap and to unify aligned, related structure (represented as a
single
deep red hexagon formed from two trapezoids in Figure 0.1).
 Figure 0.1. Spatial synthesis: abstract representation. |
One well known classical approach to this style of scholarship appears in the work of Eratosthenes of Alexandria (c. 276-194 B.C.). Eratosthenes made critical discoveries in both mathematics and geography that might seem unrelated. His prime number sieve (see Chapter 3 of this work for more detail) permitted the complete characterization of all whole numbers and offered, therefore, an understanding of the whole number system. The idea of understanding a whole, that one could never see, also applies to his measurement of the circumference of the Earth. In his role as Librarian of the great library of Alexandria, he had access to works of his many outstanding predecessors. He worked with spherical geometry, latitude and longitude, earth-sun relations, and a variety of geometric and trigonometric ideas. Eratosthenes sealed the gap between number theory and the real world with the idea of using abstract tools to understand more than what one could see, be that an infinity of whole numbers or an Earth larger than a hometown; his brain was wider than his sky.
The astonishing scholarship of Eratosthenes serves as a model, in a variety of ways, for this effort. The body of the text draws from disciplines in pure mathematics and aligns them with real world material. The underlying mathematics is critical to the effort. Beyond the synthesis of apparently disparate disciplines, however, is the model of Eratosthenes the librarian. In our present world, each of us is an amateur librarian in the great virtual library of the Internet. Direct access to materials from all over the world is available on our desktops. Thus, where possible, we assemble a subset of this library in this electronic book. The eBook, itself, serves therefore not only as an interactive forum employing state-of-the-art techniques for communicating scientific information, but also as a library on the topic it covers. Thus, we dedicate this effort to the spirit of Eratosthenes of Alexandria: may his research strategy endure for many more millennia!