• Given a sphere and a plane.  There are only a few logical possibilities about the relationship between the plane and the sphere.
• The sphere and the plane do not intersect.
• The plane touches the sphere at exactly one point:  the plane is tangent to the sphere.
• The plane intersects the sphere.
• and does not pass through the center of the sphere:  in that case, the circle of intersection is called a small circle.
• and does pass through the center of the sphere:  in that case, the circle of intersection is as large as possible and is called a great circle.
• Great circles are the lines along which distance is measured on a sphere:  they are the geodesics on the sphere.
• In the plane, the shortest distance between two points is measured along a line segment and is unique.
• On the sphere, the shortest distance between two points is measured along an arc of a great circle.
• If the two points are not at opposite ends of a diameter of the sphere, then the shortest distance is unique.
• If the two points are at opposite ends of a diameter of the sphere, then the shortest distance is not unique:  one may traverse either half of a great circle.  Diametrally opposed points are called antipodal points:  anti+pedes, opposite+feet, as in drilling through the center of the Earth to come out on the other side.
• To reference measurement on the Earthsphere in a systematic manner, introduce a coordinate system.
• One set of reference lines is produced using a great circle in a unique position (bisecting the distance between the poles):  the Equator.  A set of evenly spaced planes, parallel to the equatorial plane, produces a set of evenly spaced small circles, commonly called parallels.  They are called that because it is the planes that are parallel to each other.
• Another set of reference lines is produced using a half of a great circle, joining one pole to another, that has a unique position:  the half of a great circle that passes through the Royal Observatory in Greenwich, England (three points determine a circle).  Here it is historical consideration that produces the uniqueness in selection.  Choose a set of evenly spaced halves of great circles obtained by rotating the diametral plane along the polar axis of the Earth.  These lines are called meridians:  meri+dies=half day, the situation of the Earth at the equinoxes (see page on seasons).  The unique line is called the Prime Meridian; other halves of great circles are called meridians.
This particular reference system for the Earth is not unique; an infinite number is possible.  There is abstract similarity between this particular geometric arrangement and the geometric pattern of Cartesian coordinates in the plane.
• To use this arrangement, one might describe the location of a point, P, on the Earthsphere as being at the 3rd parallel north of the Equator and at the 4th meridian to the west of the Prime Meridian.  While this might serve to locate P according to one reference system, someone else might employ a reference system with a finer mesh (halving the distances between success lines) and for that person, a correct description of the location of P would be at the 6th parallel north of the Equator and at the 8th meridian to the west of the Prime Meridian.  Indeed, an infinite number of locally correct designations might be given for a single point:  an unsatisfactory situation in terms of being able to replicate results.  The problem lies in the use of a relative, rather than an absolute, locational system.
• To convert this system to an absolute system, that is replicable, employ some commonly agreed upon measurement strategy to standardize measurement.  One such method is the assumption that there are 360 degrees of angular measure in a circle.
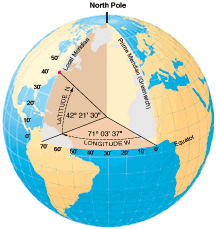
• Thus, P might be described as lying 42 degrees north of the equator, and 71 degrees west of the Prime Meridian.  The degrees north are measured along a meridian; the degrees west are measured along the Equator or along a parallel (the one at 42 north is another natural choice).  The north/south angular measure is called Latitude; the east/west angular measure is called Longitude.
• The use of standard circular measure creates a designation that is unique for P; at least unique to all whose mathematics rests on having 360 degrees in the circle.

Parts of degrees may be noted as minutes and seconds, or as decimal degrees. A degree (°) of latitude or longitude can be subdivided into 60 parts called minutes ('). Each minute can be further subdivided into 60 seconds ("). Thus,  42 degrees 30 minutes is the same as 42.50 degrees because 30/60 = 50/100.  Current computerized mapping software often employs decimal degrees as a default; older printed maps may employ degrees, minutes, and seconds.  Thus, the human mapper needs to take care to analyze the situation and make appropriate conversions prior to making measurements of position.  Such conversion is simple to execute using a calculator.  For example, 42 degrees 21 minutes 30 seconds converts to 42 + 21/60 +30/3600 degrees = 42.358333 degrees; powers of ten replace powers of 60.

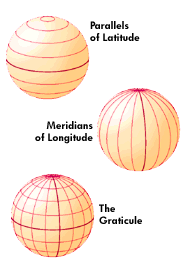
• The figure below shows the reference system described above placed on a sphere.  What might be called a Cartesian grid in the plane is called a graticule on the sphere.
• All parallels have the same latitude; they are the same distance above or below, north of or south of, the Equator.
• All meridians have the same longitude; they are the same distance east or west of the Prime Meridian.
• Spacing between successive parallels or meridians might be at any level of detail; however, when circular measure describes the position of these lines, that description is unique up to agreement to use 360 degrees in a circle.  One spacing for the set of meridians that is convenient on maps of the world, is to choose spacing of 15 degrees between successive meridians.  The reason for this is that since the meridians converge at the ends of the polar axis, that each meridian then represents the passage of one hour of time.  Given that we agree to partition a day into 24 hours, 24 times 15 is 360, meridians may also mark time.

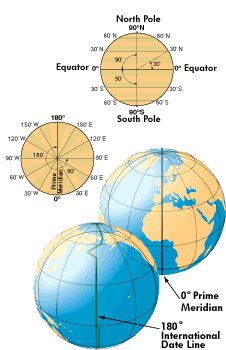
• Bounds of measurement (see the figure below).
• Latitude runs from 0° at the equator to 90°N or 90°S at the poles.
• Longitude runs from 0° at the prime meridian to 180° east or west, halfway around the globe. The International Date Line follows the 180° meridian, making a few jogs to avoid cutting through land areas.

• Length of one degree on the Earthsphere.
• One degree of latitude, measured along a meridian or half of a great circle, equals approximately 69 miles (111 km). One minute is just over a mile, and one second is around 100 feet (a pretty precise location on a globe with a circumference of 25,000 miles).   Calculation:  25,000/360 = 69.444.
• Because meridians converge at the poles, the length of a degree of longitude varies, from 69 miles at the equator to 0 at the poles (longitude becomes a point at the poles).   Calculation:  at latitude theta, find the radius, r, of the parallel, small circle, at that latitude.  The radius, R, of the Earthsphere is R = 25,000 / (2*pi)=3978.8769 miles.  Thus, cos theta = r/R (using a theorem of Euclid that alternate interior angles of parallel lines cut by a transversal are equal).  Therefore, r=R cos theta.  Then, the circumference of the small circle is 2r*pi and the length of one degree at theta degrees of latitude is 2r*pi / 360.  For another application of this particular theorem of Euclid, see the linked page concerning Eratosthenes measurement of the Earthsphere.
• For example, at 42 degrees of latitude, r =  2956.882.  Thus, the circumference of the parallel at 42 degrees north is approximately 18578.6205 miles.  Thus, the length of one degree of longitude, measured along the small circle at 42 degrees of latitude, is:  51.607 miles.
• This particular calculation scheme is a rich source of elementary problems using geometry and trigonometry.  Consider the following question:  at what latitude is the length of one degree on longitude exactly half the value of one degree of longitude at the equator?
• Readers wishing a visual review of trigonometry may find this link to be of use.

• The position of the sun in the sky.  On June 21, the direct ray of the sun is overheard, or perpendicular to a plane tangent to the Earthsphere, at 23.5 degrees north latitude (link to page about seasons).  The angle of the sun in the sky at noon on that day is 90 degrees.  What is the angle of the sun in the sky, at noon on June 21, at 42 degrees north latitude?  Again, simple geometry and trigonometry solve the problem for this value and for any other.   Use the fact that 42-23.5=18.5 degrees; that there are 180 degrees in a triangle (look for a right triangle with the right angle at 42 degrees north latitude); and that corresponding angles of parallel lines cut by a transversal are equal.  The answer works out to be 71.5 degrees.  Thus, on June 21 at local noon, in the northern hemisphere at 42 degrees north latitude the sun will appear in the south at 71.5 degrees above the horizon; in the southern hemisphere at 42 degrees south it will appear in the northern sky at 71.5 degrees above the horizon.  Between the tropics, some interesting situations prevail (link to Parallels between Parallels, pages 74-86, IMaGe Monograph 13).  Use of this technique is important in calculating shadow and related matters in electronic mapping:  it was employed in making several virtual reality models of in this book.

Further Directions:

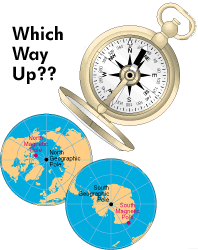
• The north and south poles are the earth's geographic poles, located at each end of its axis of rotation. All meridians meet at these poles. The compass needle points to either of the earth's two magnetic poles. The north magnetic pole is located in the Queen Elizabeth Islands group, in the Canadian Northwest Territories. The south magnetic pole lies near the edge of the continent of Antarctica, off the Adélie Coast. The magnetic poles are constantly moving.   What are the implications of this fact for the stability of our graticule?

• All of our geometric analysis is based on Euclidean geometry, assuming Euclid's Parallel Postulate:  given a line and a point not on the line--through that point there passes exactly one line that does not intersect the given line.  Non-Euclidean geometries violate this Postulate.  What does the geometry of the Earthsphere become in the non-Euclidean world?