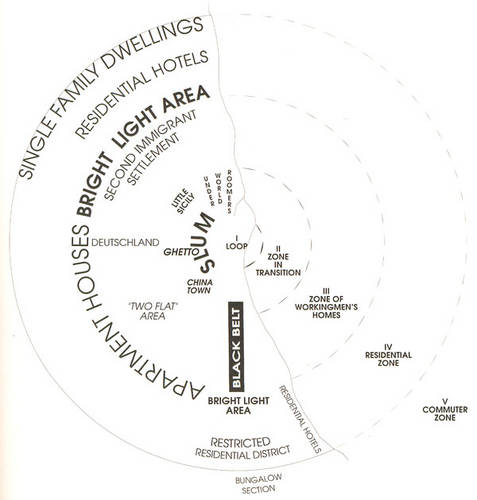
 Figure 1. Burgess Concentric Ring model of Chicago population patterns in the 1920s (Park and Burgess, 1925, p. 55). |
 Figure 1. Burgess Concentric Ring model of Chicago population patterns in the 1920s (Park and Burgess, 1925, p. 55). |
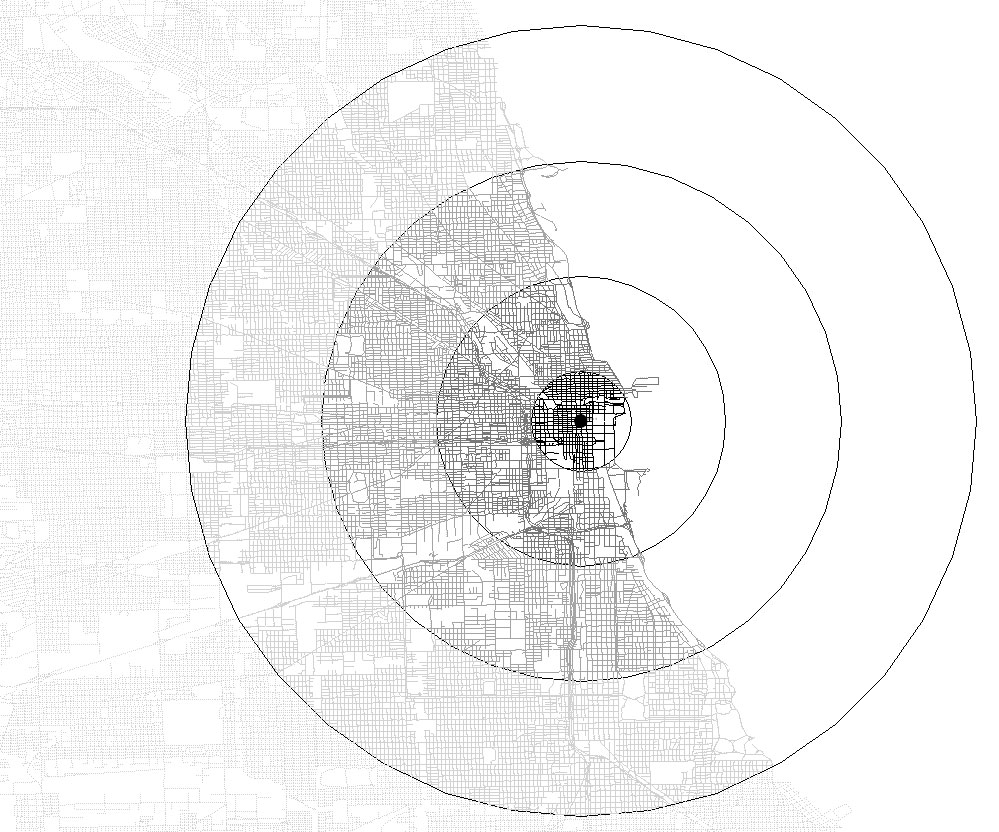 Figure 2.
Contemporary Tiger files of the Chicago street network overlain with
Burgess concentric rings positioned as suggested in Figure 1.
|
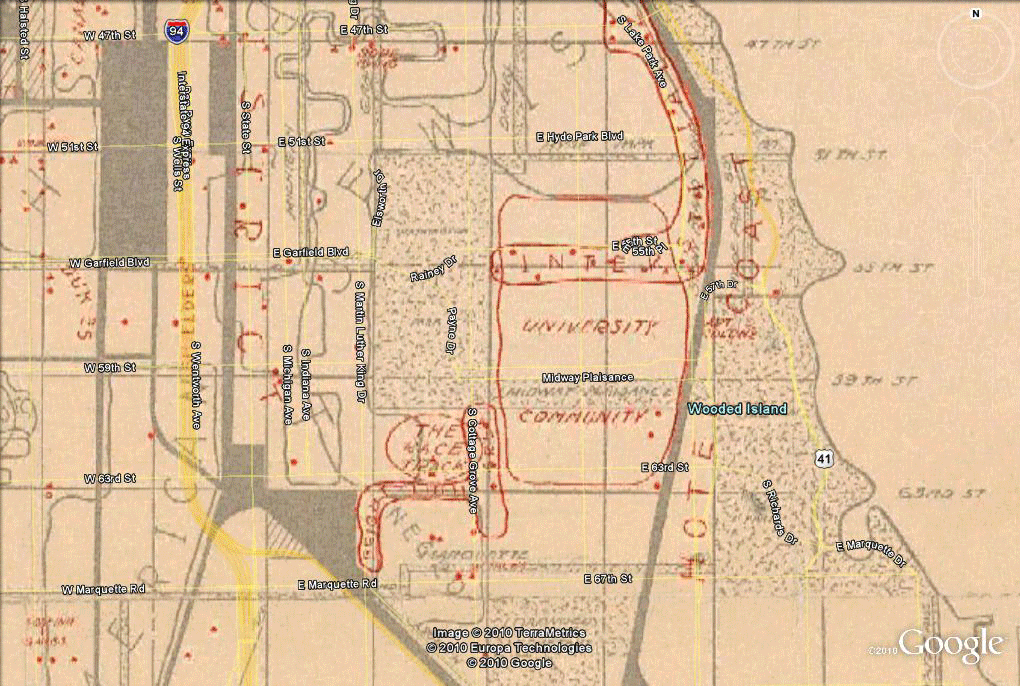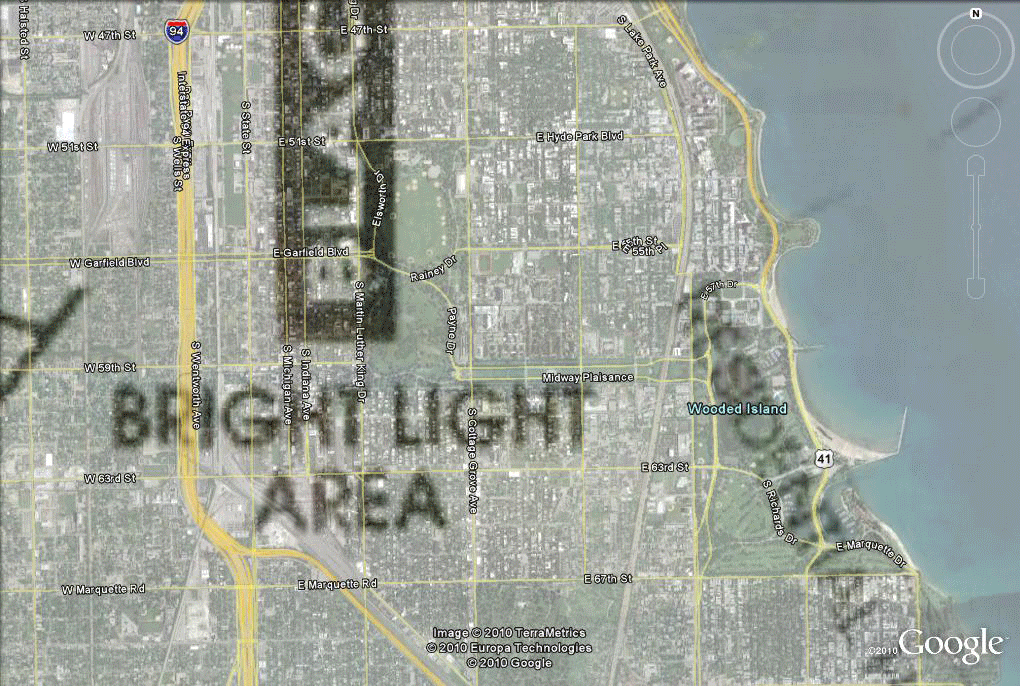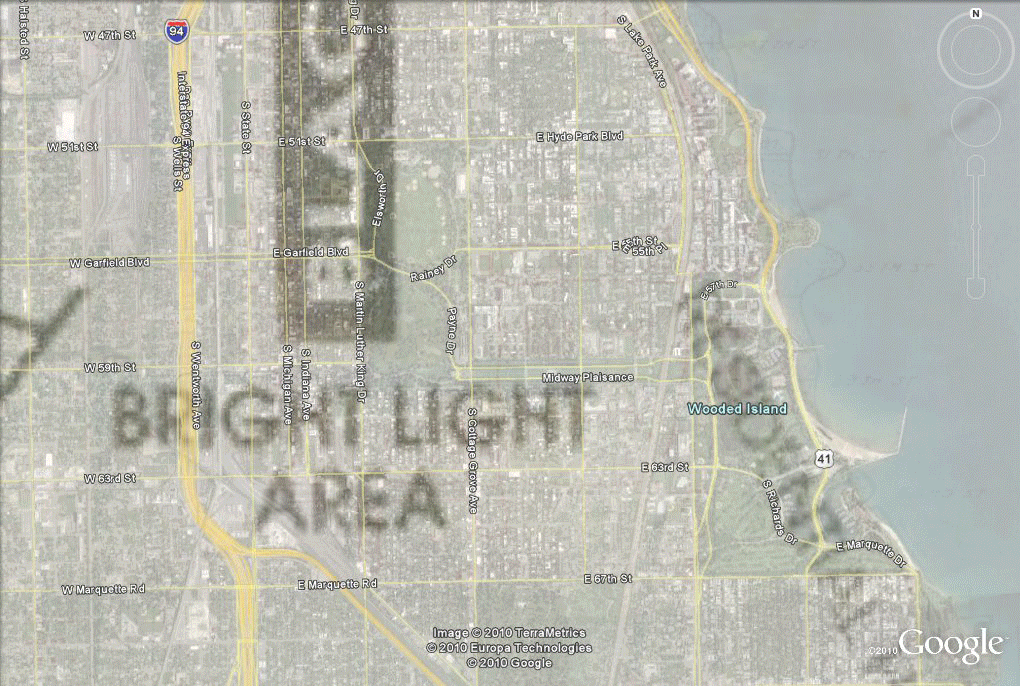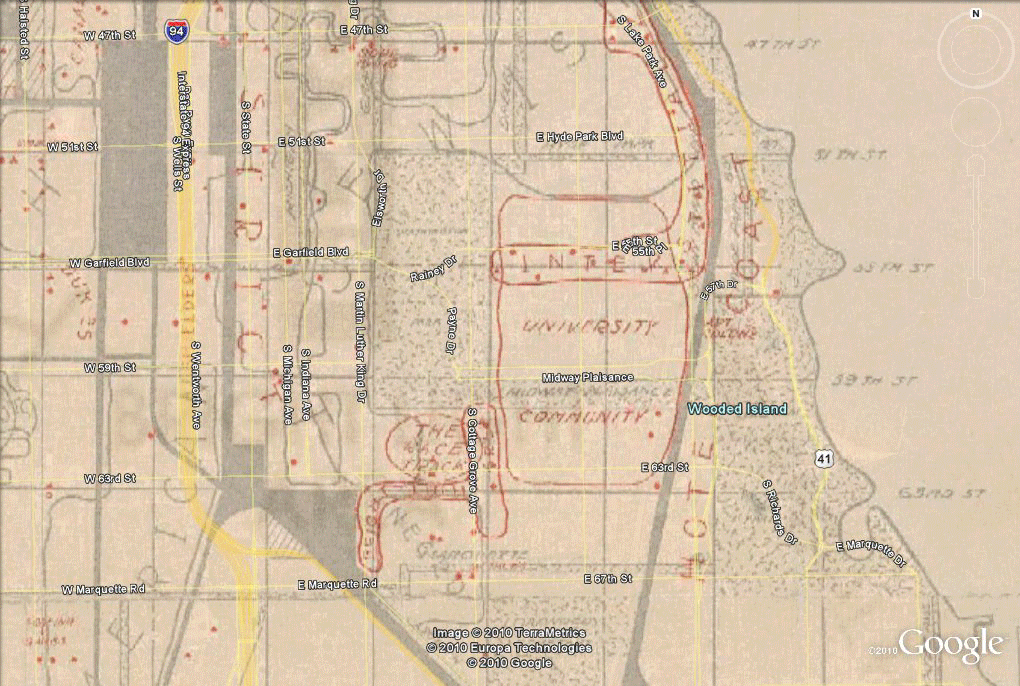 Figure 3. Alignment of a Gangland map of the 1920s with Tiger files of today and the Burgess model of Figure 1, all superimposed as layers in Google Earth which permits the easy stretching of scanned images to fit the underlying Google Earth globe. |
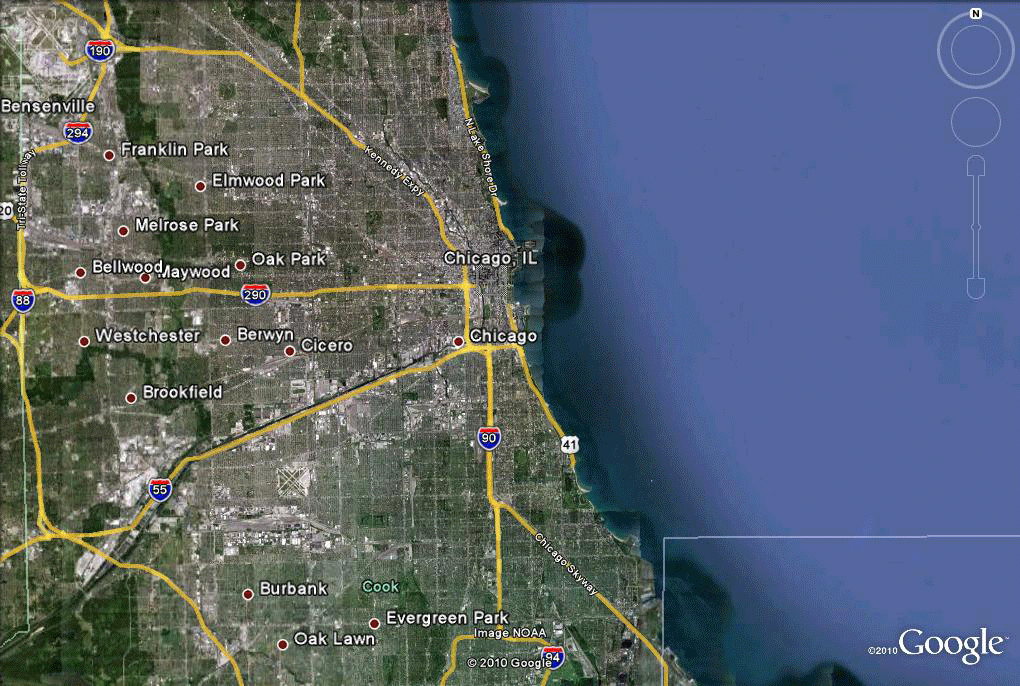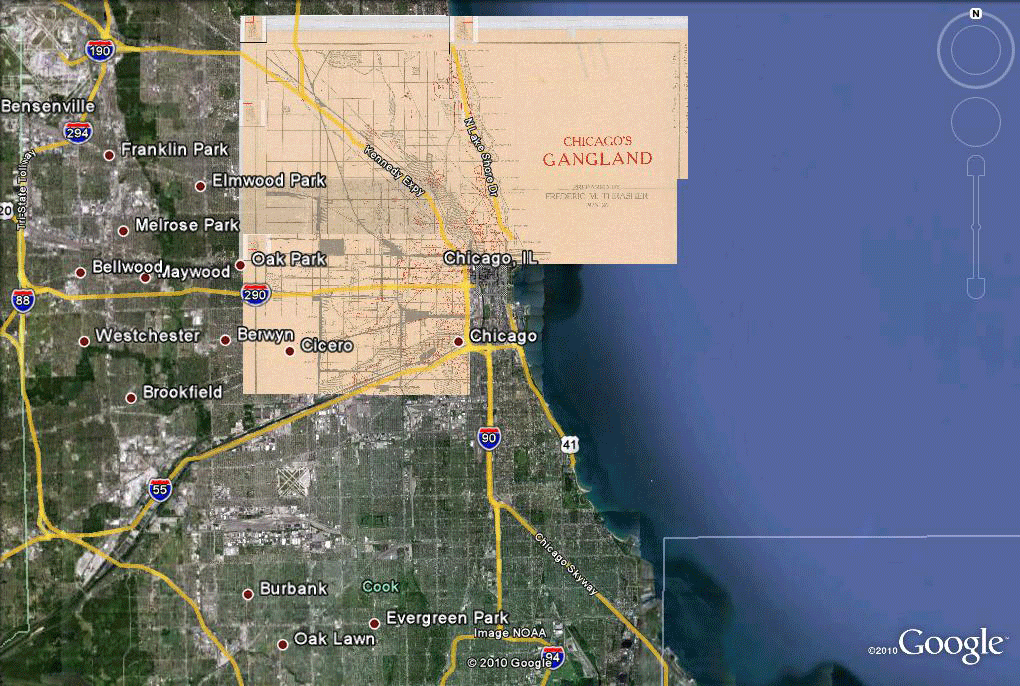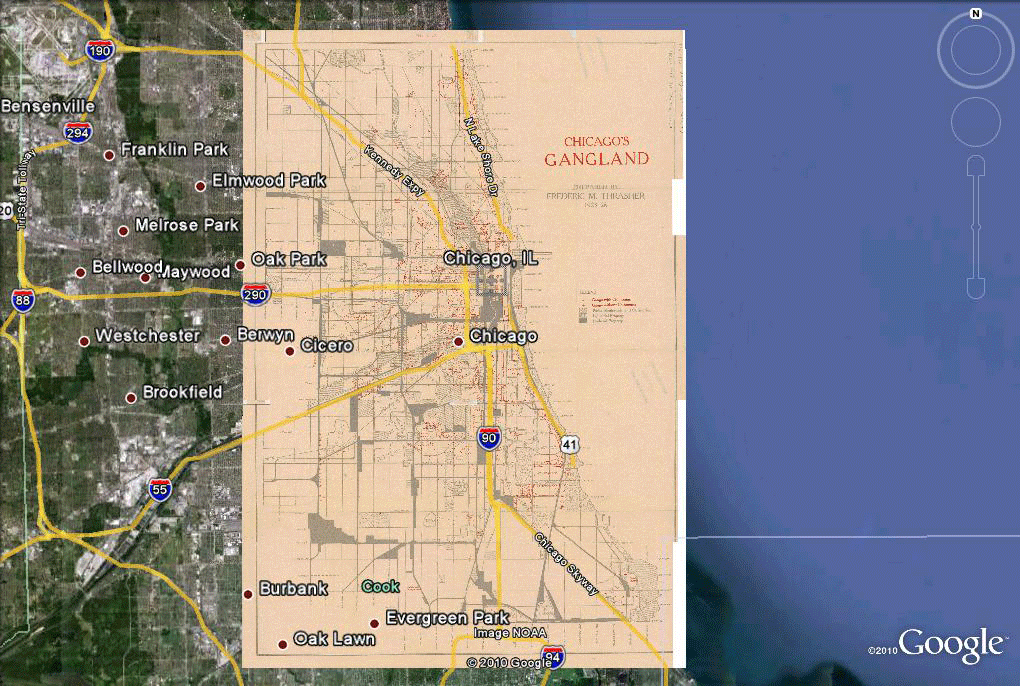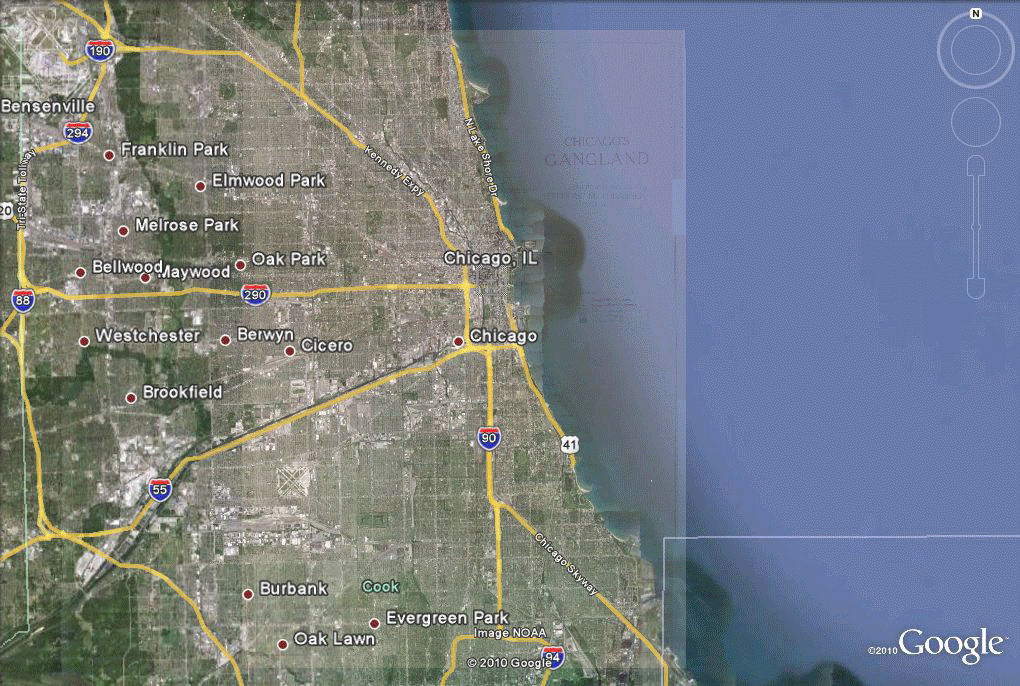 Figure 4. Insertion of flat Gangland map in Google Earth, aligned to underlying features, using the concept of "gores" or small sections reducing error in fit. |
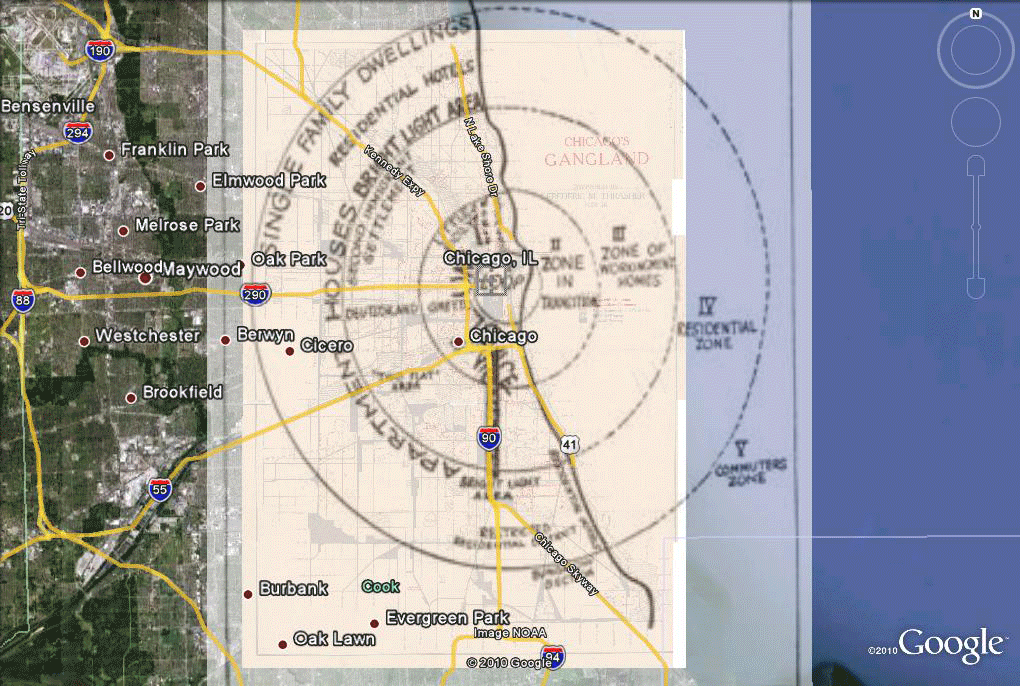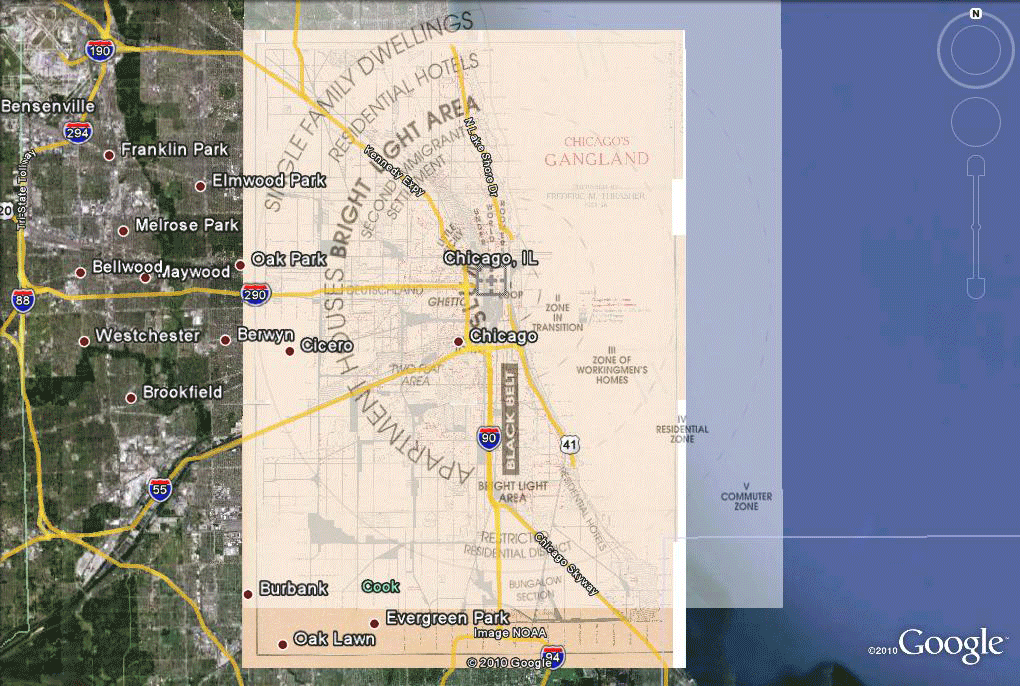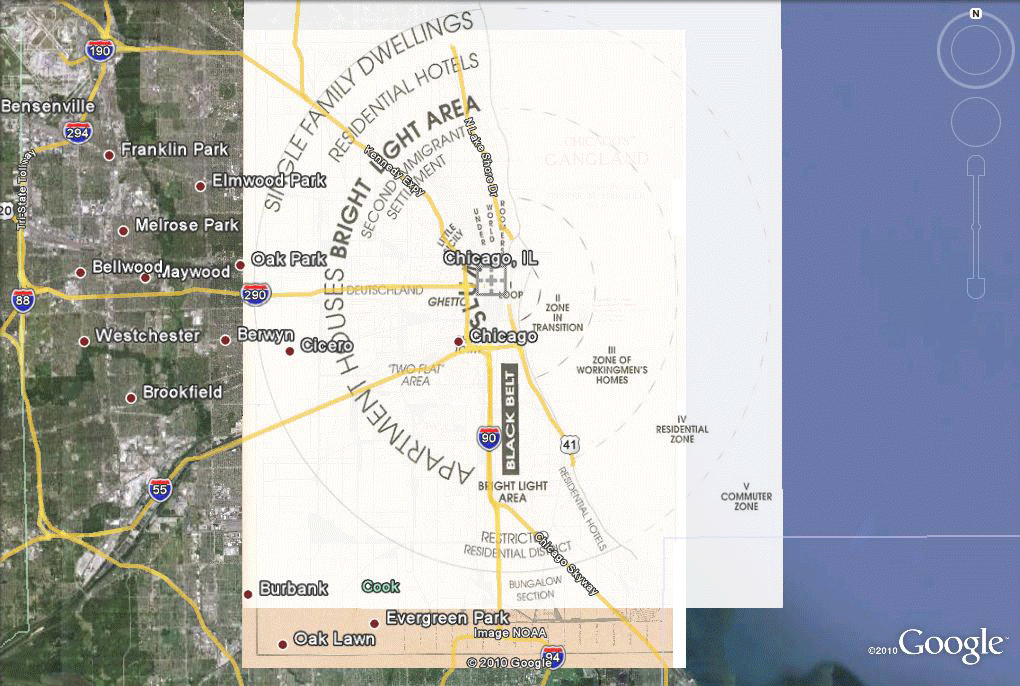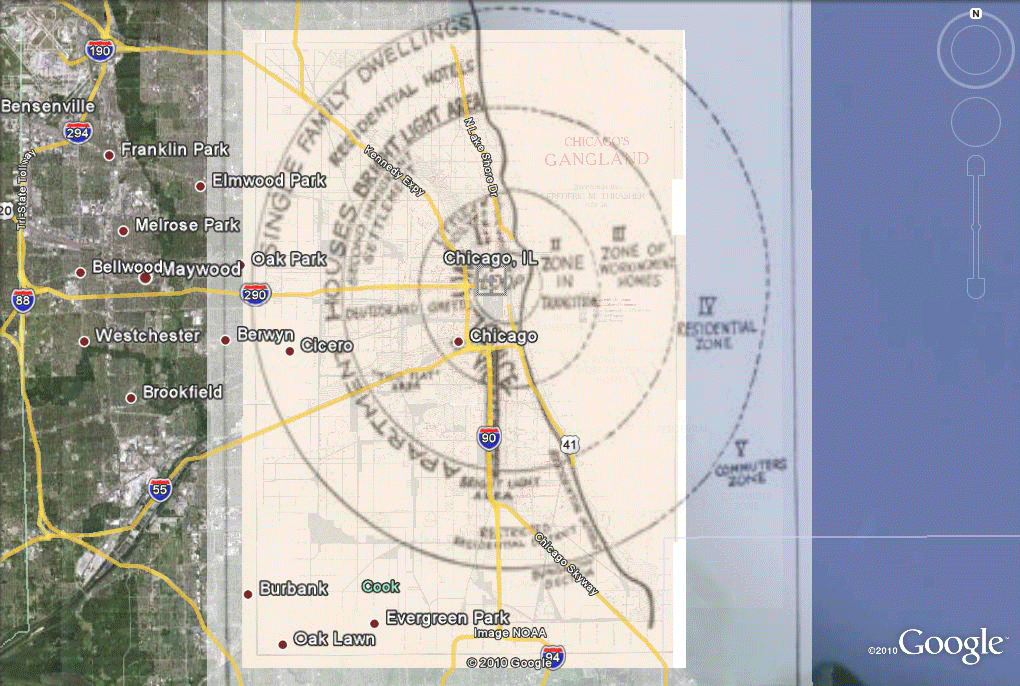 Figure 5. Alignment of the Burgess model with the Gangland map and therefore with Google Earth and associated Tiger files. |
Figure 6. Interactive display subject to partial reader control. |
| Solstice:
An Electronic Journal of Geography and Mathematics,
Volume XXI, Number 2 Institute of Mathematical Geography (IMaGe). All rights reserved worldwide, by IMaGe and by the authors. Please contact an appropriate party concerning citation of this article: sarhaus@umich.edu http://www.imagenet.org http://deepblue.lib.umich.edu/handle/2027.42/58219  |
 IMaGe logo designed
by Allen K. Philbrick from an original provided by the Founder. IMaGe logo designed
by Allen K. Philbrick from an original provided by the Founder.
|
|
Congratulations to all Solstice contributors. |
|
| Remembering those who
are gone now but who contributed in various ways to Solstice or to IMaGe
projects, directly or indirectly, during the first 25 years of IMaGe: Allen K. Philbrick | Donald F. Lach | Frank Harary | William D. Drake | H. S. M. Coxeter | Saunders Mac Lane | Chauncy D. Harris | Norton S. Ginsburg | Sylvia L. Thrupp | Arthur L. Loeb | George Kish | |