 |
 |
Circular
regions
surrounding lattice points
A
scatter
of points, spread evenly across the plane, may take on a variety
of configurations.
If one wishes to consider circular buffers around each point,
then these
buffers may overlap or be widely spaced. The space between
buffers,
in the background behind them, is interstitial space separating
buffers.
A natural issue to consider is to minimize interstitial space
and provide
some sort of maximal coverage of the plane by the buffers:
to provide
a "close packing" of the plane by circles.
Two close packings of the plane with
circles
of identical radius are shown in Figure 1.1: one with
circles centered
on a square lattice and the other with circles centered on a
triangular
lattice.
 |
 |
Figure 1.1 left, right. Animation shows square and triangular lattices in the plane and associated close packings with circles of identical radius. (Source of base image, no longer present at the cited url:http://www.psc.edu/~burkardt/src/graph_paper/graph_paper.html graph paper showing grid, triangular and hexagonal regions, John Burkardt, Pittsburgh Supercomputing Center, Carnegie Mellon University, University of Pittsburgh.).
It is a straightforward matter to
calculate
the interstitial space between circles associated with a square
of side
x
in the square lattice and a corresponding parallelogram of side
x
in the triangular lattice. The radius of the circles in
each figure
is therefore x/2 and the area of the circles pi*x2/4.
Figure
1.2 shows a calculation of interstitial space: there is
less
interstitial area, between circles, within the parallelogram
than there
is within the square. Extrapolating this idea across the
plane, one
imagines naturally that the close packing of circles on the
triangular
lattice is denser than is the close packing of circles on the
square lattice.
| Side of length x, both square and parallelogram. Radius of any circle is x/2. | Area of any circle is pi*x2/4 |
 |
Red
Area = area of square with four one-quarter circular
sectors subtracted
out = area of square with one full circular area
subtracted out.
Area of square: x2
|
 |
Red
Area=area of parallelogram with two one-third circles
and two one-sixth
circular sectors subtracted out = area of
parallelogram with one full circular
area subtracted out.
Area
of parallelogram:
x Since |
Figure 1.2. There is less interstitial area between circles within the parallelogram than there is between circles within the square. (Source of base image, no longer present at the cited url:http://www.psc.edu/~burkardt/src/graph_paper/graph_paper.html graph paper showing grid, triangular and hexagonal regions, John Burkardt, Pittsburgh Supercomputing Center, Carnegie Mellon University, University of Pittsburgh.).
This chain of reasoning indicates that the close packing of the plane by circles of identical radius is denser for a triangular lattice than it is for a square lattice. Gauss (1831) proved that, in fact, the densest lattice packing of the plane is the one based on the triangular lattice. In 1940, Fejes-Toth proved that that same packing is not only the densest lattice packing of the plane but is also the densest of all possible plane packings.
If one thinks, then, of the circles as if they were bubble-foam, the circles centered on a square grid pattern expand and collide to form a grid of squares (suggested in the top figure in Figure 1.2). The circles centered on a triangular grid pattern expand and collide to form a mesh of regular hexagons (suggested in the bottom figure in Figure 1.2). Because the close packing of circles centered on points spaced in a triangular grid is the densest possible close packing of the plane, the space-filling pattern of hexagonal cells associated with that packing also possesses unique character. If one were to enter a square or triangular grid into Geographic Information System software, and ask the software to calculate Thiessen polygons the grid of square cells would emerge from the square lattice and the grid of hexagonal cells would emerge from the triangular lattice. Thus, these cells can arise in a number of technical ways.
The theoretical issues surrounding tiling in the plane are complex; even deeper are those issues involving packings in three dimensional space. We confine our interest in that matter to simply illustrating Gauss's methods and stating Fejes-Toth's extension of it. The reader interested in probing this topic further is referred to the references. Interpretation of the simple triangular grid has range sufficient to fill this volume and more.
Basic
assumptions
One
classical
interpretation of what dots on a lattice might represent is
found in the
geometry of "central place theory." Readers interested in
the development
of this theory, over time and with regard to a clear
understanding of who
did what and when it was done, are referred to the
references. We
simply present some of the ideas in order to focus on the
geometry.
Geometric central place models take the complex human process of
urbanization
and look at it in an abstract theoretical form in order to
uncover principles
which might endure despite changes over time, situation,
cultural tradition,
and all the various human elements that are truly the hallmarks
of urbanization.
Simplicity helps to reveal form: models are not
representations of
reality. They do, however, offer a way to look at some
structural
elements of complexity. Thus, consider dots on a
triangular lattice
as populated places (often, villages). Circles, expanding
into hexagons,
are areas that are tributary to the populated places. In
the traditional
formulation (described after Kolars
and
Nystuen) one considers four basic postulates (no one of
which is
"real" but each of which is simple):
Suppose, in a triangular lattice of
villages, that one village adds to its retailing
activities. After
some time, growth occurs elsewhere. How might other
villages compete
to serve tributary areas: how will the larger, new
villages share
the tributary area? The answers lead to a surprising
number of possible
scenarios. Figure 1.3 shows the first in an infinite
number of possibilities.
Animated locations, for competing larger villages, are shown in
Figure
1.3. The smallest villages are represented as small red
dots; next
nearest neighbors competing for intervening red dots are
represented in
blue; and, next nearest neighbors competing for intervening blue
dots are
represented in green. Of course, one is usually only
willing to travel
so far to go to a place only slightly larger, so the fact that
the animated
pattern could be extended to an infinite number of levels,
beyond green,
may not mirror the second postulate. Over time, however,
one might
suppose further growth and an entire hierarchy of populated
places.
 |
Figure 1.3. A triangular lattice of dots with animated locations for competing locations entering and vanishing from the picture.
Such a view of growth leads to another set of assumptions (after Christaller).
Marketing
principle:
K=3
Consider a
central
place point, A, in a triangular lattice (Figure
1.4). Unit
hexagons (fundamental cells) surround each of the points in the
lattice
and represent the small tributary area of each village (red
hexagons in
Figure 1.5a). Growth at A has distinguished it
from other
villages in the system. It will now serve a tributary area
larger
than will the unit hexagon. There are six villages directly
adjacent to
A.
The unit hexagons represent a partition of area based on even
sharing of
area between A and these six villages. When
A expands
its central place activities, others may also desire to do so as
well.
Figure 1.4 shows the locations for the next nearest competitors,
such as
A' in blue, to enter the system. Given that they, too,
will share
area evenly, a set of larger hexagons emerges (blue hexagons in
Figure
1.5a). The competitors that enter are spaced at a
distance,
in terms of lattice points spaced one unit apart, of ![]() units (Figure 1.4). The position of the competitors that
enter the
system in this scenario are as close as possible to A;
expansion
of goods and services at any of the six closest neighbors would
constitute
no change in basic pattern. One might imagine, therefore,
that emphasis
on distance minimization optimizes marketing
capability--distance to market
is at a minimum. Figure 1.5a shows the unit hexagons
and the
larger hexagons based on expansion of goods and
services. To
get a view of a large scatter of dots, arranged according to
this idea,
consider the
linked virtual reality
model.
Use the Viewpoints to see an overview and a closeup; drive
through it on
your own.
units (Figure 1.4). The position of the competitors that
enter the
system in this scenario are as close as possible to A;
expansion
of goods and services at any of the six closest neighbors would
constitute
no change in basic pattern. One might imagine, therefore,
that emphasis
on distance minimization optimizes marketing
capability--distance to market
is at a minimum. Figure 1.5a shows the unit hexagons
and the
larger hexagons based on expansion of goods and
services. To
get a view of a large scatter of dots, arranged according to
this idea,
consider the
linked virtual reality
model.
Use the Viewpoints to see an overview and a closeup; drive
through it on
your own.
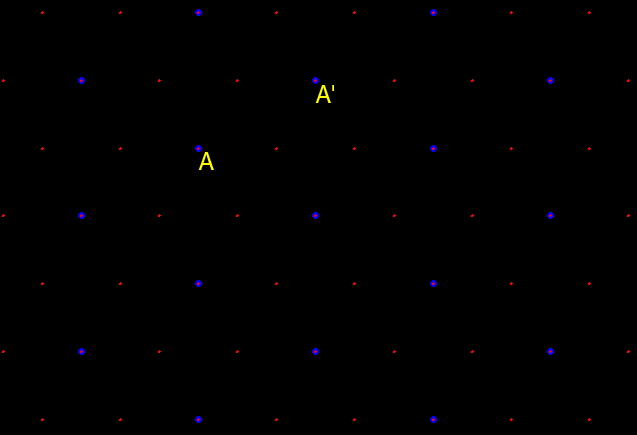 |
Figure 1.4. K=3:
Marketing. Distance measurement between adjacent
competing
new centers, A and A': in this case,
competing centers,
blue dots, are spaced ![]() units
apart, assuming a distance of one unit between adjacent red
dots.
units
apart, assuming a distance of one unit between adjacent red
dots.
Thus, when competitors are chosen in
this
manner, the pattern of one layer of hexagons, in relation to
another, has
become known as a hierarchy arranged according to a "marketing
principle"
(Figure 1.5a). Notationally, it is captured by the square
of the
distance between competing centers: as a "K=3"
hierarchy (Figure
1.4). Each large hexagon contains the equivalent of three
smaller
hexagons. One large hexagon = 1 small hexagon + six copies
of 1/3
of a small hexagon = 3 small hexagons (Figure 1.5b, c, and
d). Thus,
the value K=3 is not only related to distance between
competing
centers but also to size of tributary areas generated by
competition:
as a constant of the hierarchy.

Figure 1.5a. K=3 hierarchy showing three layers of a nested hierarchy of hexagons of various sizes oriented with respect to one another according to the distance principle illustrated in Figure 1.4. |

Figure 1.5b. Each blue hexagon contains the equivalent of three red hexagons: one entire red hexagon surrounded by six copies of 1/3 of a red hexagon. |

Figure 1.5c. Each green hexagon contains the equivalent of three blue hexagons: one entire blue hexagon surrounded by six copies of 1/3 of a blue hexagon. |

Figure 1.5d. The green hexagons contain the equivalent of 31 blue hexagons and 32 red hexagons. |
Figure 1.5.
Back
to Chapter 2 K=3 reference.
Figure 1.6 shows the locations for
the
next nearest competitors, next beyond those from K=3, to
enter the
system. Given that they, too, will share area evenly, a
set of even
larger hexagons emerges. Figure 1.7a shows the unit
hexagons
and the larger hexagons based on expansion of goods and
services.
The competitors that enter are spaced at a distance, in terms of
lattice
points spaced one unit apart, of 2 units (Figure 1.6). The
position
of the competitors that enter the system in this scenario lie
along radials
that fan outward from A and pass along existing
boundaries to tributary
areas. One might imagine, therefore, that emphasis on
market penetration,
or transportation, is the focus here. To get a view of a
large scatter
of dots, arranged according to this idea, consider the linked
virtual reality model. Use the Viewpoints to see an
overview and
a closeup; drive through it on your own.
 |
Figure 1.6. K=4: Marketing. Distance measurement between adjacent competing new centers, A and A' is 2 units, in this case (assuming a distance of 1 unit between adjacent red dots).
Thus, when competitors are chosen in
this
manner, the pattern of one layer of hexagons, in relation to
another, has
become known as a hierarchy arranged according to a
"transportation principle"
(Figure 1.7a). Notationally, it is captured by the square
of the
distance between competing centers: as a "K=4"
hierarchy (Figure
1.6). Each large hexagon contains the equivalent of four
smaller
hexagons. One large hexagon = 1 small hexagon + six copies
of 1/2
of a small hexagon = 4 small hexagons (Figure 1.7b, c, d).
Thus,
the value K=4 is not only related to distance between
competing
centers but also to size of tributary areas generated by
competition--as
a constant of the hierarchy.

Figure 1.7a. K= 4 hierarchy showing three layers of a nested hierarchy of hexagons of various sizes oriented with respect to one another according to the distance principle illustrated in Figure 1.6. |
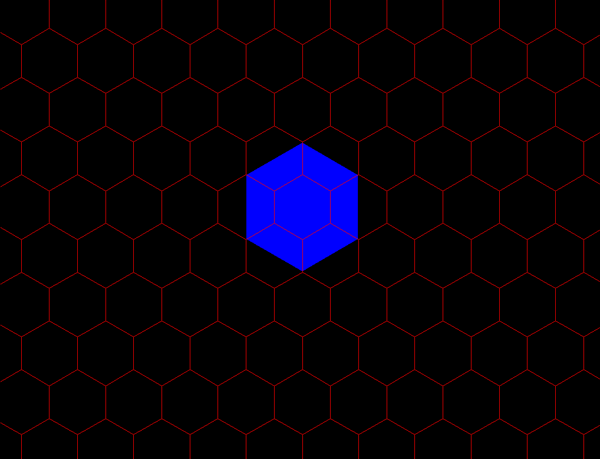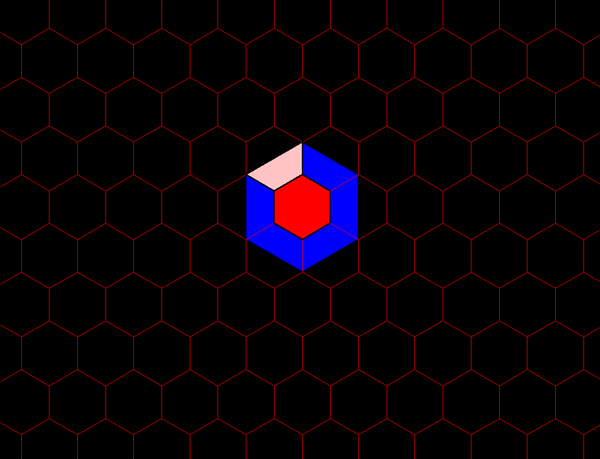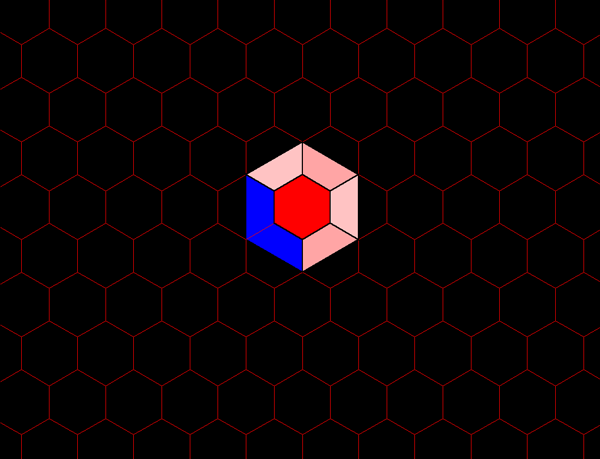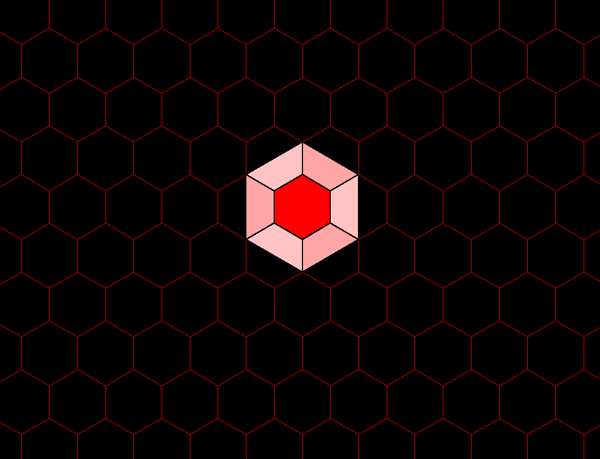
Figure 1.7b. Each blue hexagon contains the equivalent of four red hexagons: one entire red hexagon surrounded by six copies of 1/2 of a red hexagon. |

Figure 1.7c. Each green hexagon contains the equivalent of four blue hexagons: one entire blue hexagon surrounded by six copies of 1/2 of a blue hexagon. |

Figure 1.7d. The green hexagons contain the equivalent of 41 blue hexagons and 42 red hexagons. |
Figure 1.7.
Back
to Chapter 2 K=4 reference.
Administrative
principle:
K=7
Figure 1.8 shows the locations for
the
next nearest competitors, next beyond those from K=4, to
enter the
system. Given that they, too, will share area evenly, a
set of even
larger hexagons emerges. Figure 1.9a shows the unit
hexagons
and the larger hexagons based on expansion of goods and
services.
The competitors that enter are spaced at a distance, in terms of
lattice
points spaced one unit apart, of ![]() units (Figure 1.8). The position of the competitors that
enter the
system in this scenario create larger hexagons whose boundaries
pass through
very few other populated places: hence, top-down control,
or rule
from the center is emphasized. One might imagine,
therefore, an emphasis
on administrative control here. To get a view of a large
scatter
of dots, arranged according to this idea, consider the linked
virtual reality model. Use the Viewpoints to see an
overview and
a closeup; drive through it on your own.
units (Figure 1.8). The position of the competitors that
enter the
system in this scenario create larger hexagons whose boundaries
pass through
very few other populated places: hence, top-down control,
or rule
from the center is emphasized. One might imagine,
therefore, an emphasis
on administrative control here. To get a view of a large
scatter
of dots, arranged according to this idea, consider the linked
virtual reality model. Use the Viewpoints to see an
overview and
a closeup; drive through it on your own.
 |
Figure 1.8. K=7:
Marketing. Distance measurement between adjacent
competing
new centers, A and A' is ![]() (assuming a distance of 1 unit between adjacent red dots).
(assuming a distance of 1 unit between adjacent red dots).
Thus, when competitors are chosen in
this
manner, the pattern of one layer of hexagons, in relation to
another, has
become known as a hierarchy arranged according to an
"administration principle"
(Figure 1.9a). Notationally, it is captured by the square
of the
distance between competing centers: as a "K=7"
hierarchy (Figure
1.8). Each large hexagon contains the equivalent of seven
smaller
hexagons. One large hexagon = 1 small hexagon + six copies
of a small
hexagon (underfit and overfit regions balance) = 7 small
hexagons (Figure
1.9b, c, d). Thus, the value K=7 is not only
related to distance
between competing centers but also to size of tributary areas
generated
by competition--as a constant of the hierarchy.

Figure 1.9a. K= 7 hierarchy showing three layers of a nested hierarchy of hexagons of various sizes oriented with respect to one another according to the distance principle illustrated in Figure 1.8. |

Figure 1.9b. Each blue hexagon contains the equivalent of seven red hexagons: one entire red hexagon surrounded by six copies equivalent to a single red hexagon. Each of the perimeter red hexagons is composed of 11/12 of a single red hexagonal cell plus 1/12 of an adjacent red cell: in an underfit/overfit pattern. |

Figure 1.9c. Each green hexagon contains the equivalent of seven blue hexagons: one entire blue hexagon surrounded by six copies equivalent to a single blue hexagon. Each of the perimeter blue hexagons is composed of 11/12 of a single blue hexagonal cell plus 1/12 of an adjacent blue cell: in an underfit/overfit pattern. |
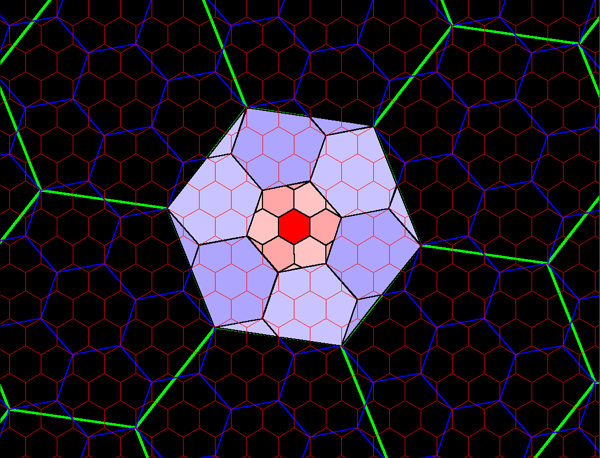
Figure 1.9d. The green hexagons contain the equivalent of 71 blue hexagons and 72 red hexagons. |
Figure 1.9.
Back
to Chapter 2 K=7 reference.
A tiled view
of each
hierarchy: mechanics of construction
The process of creating larger
hexagons,
as larger tributary areas representing expanded central place
activities,
can be carried out indefinitely. The set of figures above
(1.5, 1.7,
and 1.9) shows the general patterns that emerge and underscores,
particularly,
the importance of the constant of the hierarchy. Large
hexagons in
one layer contain the equivalent of K1
hexagons of the
next smallest size within them; they contain the equivalent of K2
hexagons from the level two layers down in the hierarchy, and so
forth.
The K value is an invariant of each geometric hierarchy
that uniquely
characterizes it. The mathematical search for invariants
as bench
marks against which to view abstract structure is equivalent to
the geographical
search for bench marks in the field (physical or human) against
which to
view mapped, spatial structure.
Virtual reality central place skylinesThe initial conditions from the real world may suggest building a hierarchy from small hamlets to large cities, in the style of Christaller, or they may suggest the reverse, in the style of Lösch (or any of an infinite number of possibilities in between--we confine ourselves to the extremes). Independent of such choice, however, the resulting geometry is identical: a pattern of hexagons of various sizes, dependent on spacing between competing centers at a given hierarchical level, is the result. To see the different initial patterns of dots, and to move them around on the screen, it is useful to capture the dot patterns above as virtual reality scenes. Animation of successive virtual reality scenes, as a sequence of screen captures of the scene from various vantage points, offers the reader a chance to examine closely the three different styles of initial dot scatter used to create the geometries of hexagons associated with K=3, K=4, and K=7.
The linked
figures,
Figures 1.L1 (derived from
Figure 1.5),
1.L2
(derived from Figure 1.7), and
1.L3 (derived
from Figure 1.9), offer a view of central place K=3, K=4,
and
K=7 landscapes as central place skylines in virtual
reality.
Links to each of these were given above, as they
developed. Here,
we simply accumulate the set in one set of links near each other
for ease
in making comparisons. Load CosmoPlayer and click on the
links to
drive through these landscapes and experience them as if the
higher order
central places represent taller urban structures, such as cell
towers or
other dominant skyline features. Figure 1.10 shows
each of
these virtual reality models, from the vantage point of "entry,"
as animated
screen capture so that one might readily compare the three
hierarchies.
Figures 1.11 and 1.12 show similar animations, for purposes of
comparison
of pattern among K=3, K=4, and
K=7, from the vantage
point of "Overview" and "Close Up" respectively.
Movies of
these animations permit the reader to control the animation
frame rate:
Movie
of 1.10,
movie of 1.11,
and movie of 1.12.
(If
the horizontal scroll bar does not show at the bottom of the
linked
image, expand your browser to show the full screen: in
Microsoft
Internet Explorer, for example, hit the F11 key.) In
the next
chapter, we use virtual reality to take a closer look at the
geometry of
these hierarchies; thus, it is worth the effort now to load the
plug-in
and to practice virtual navigation in a simple landscape.
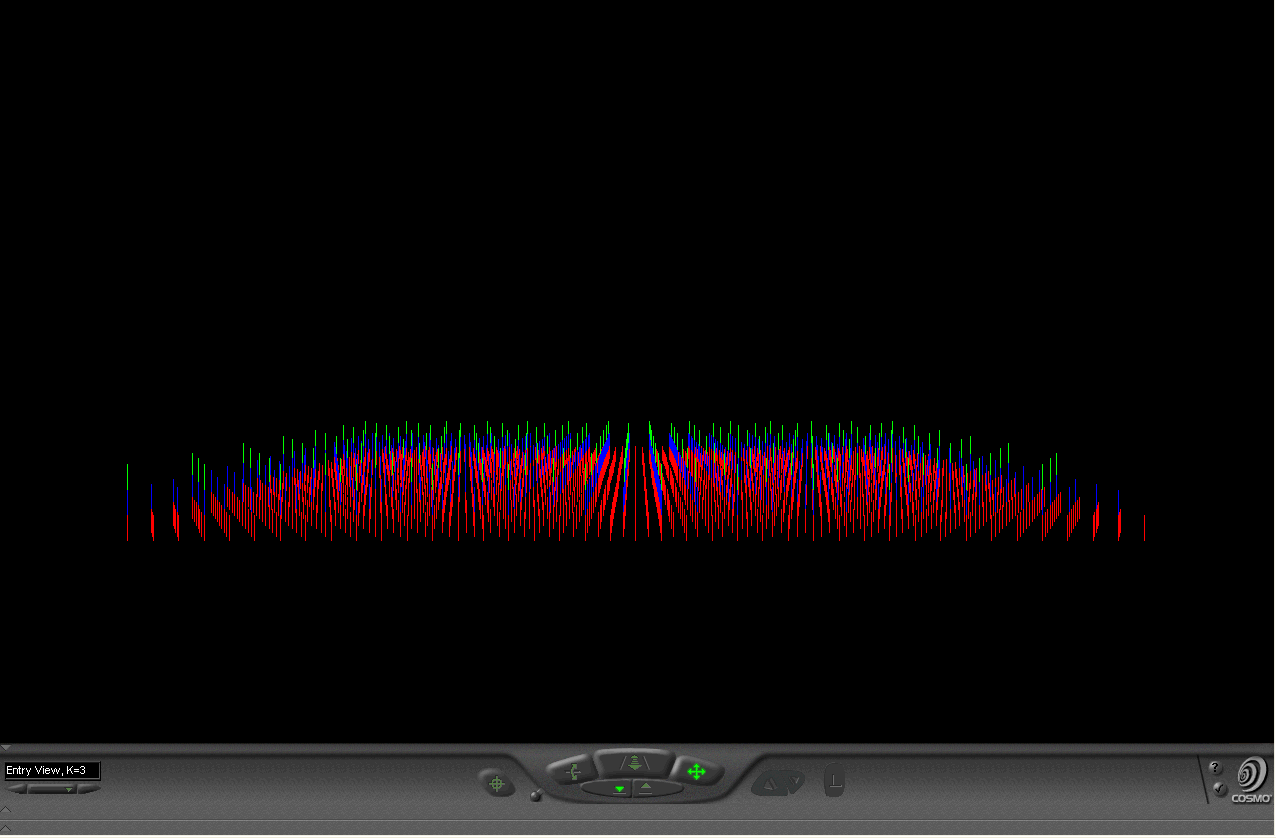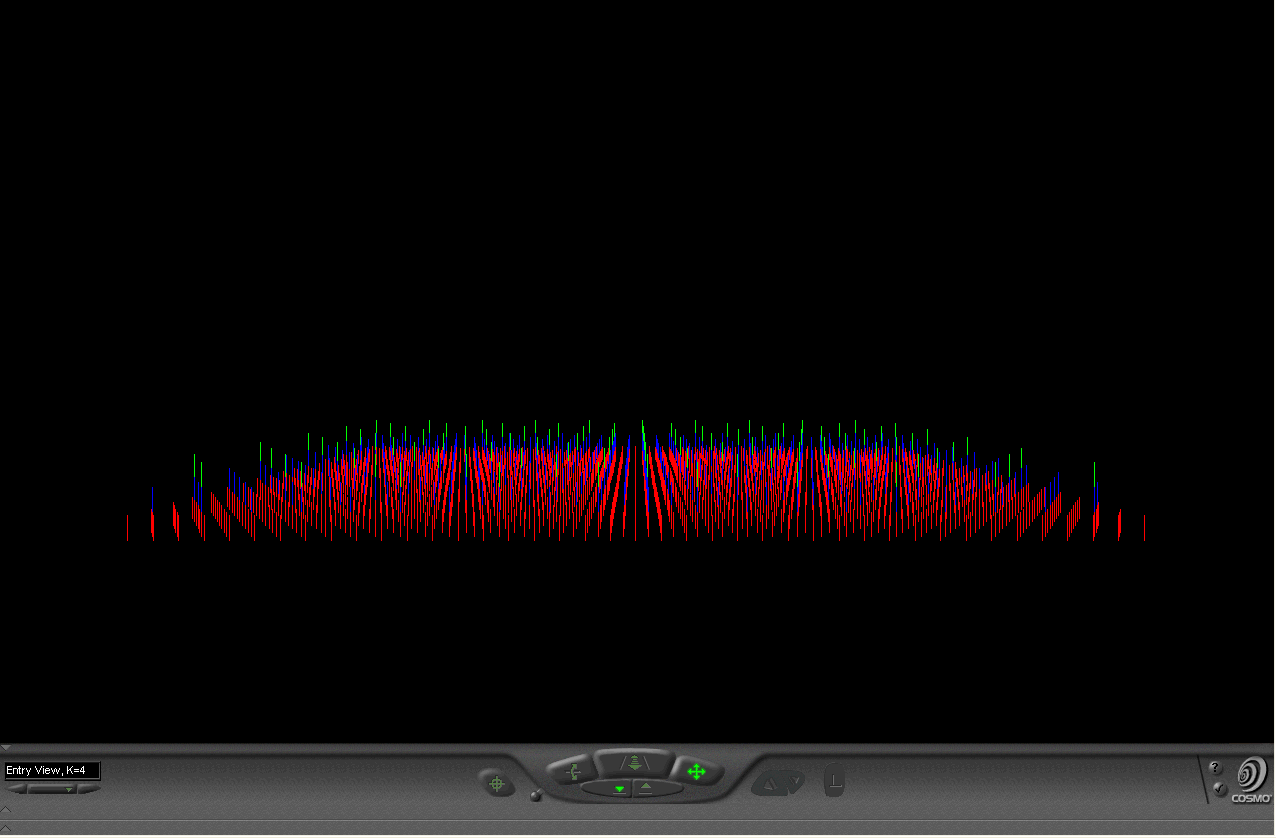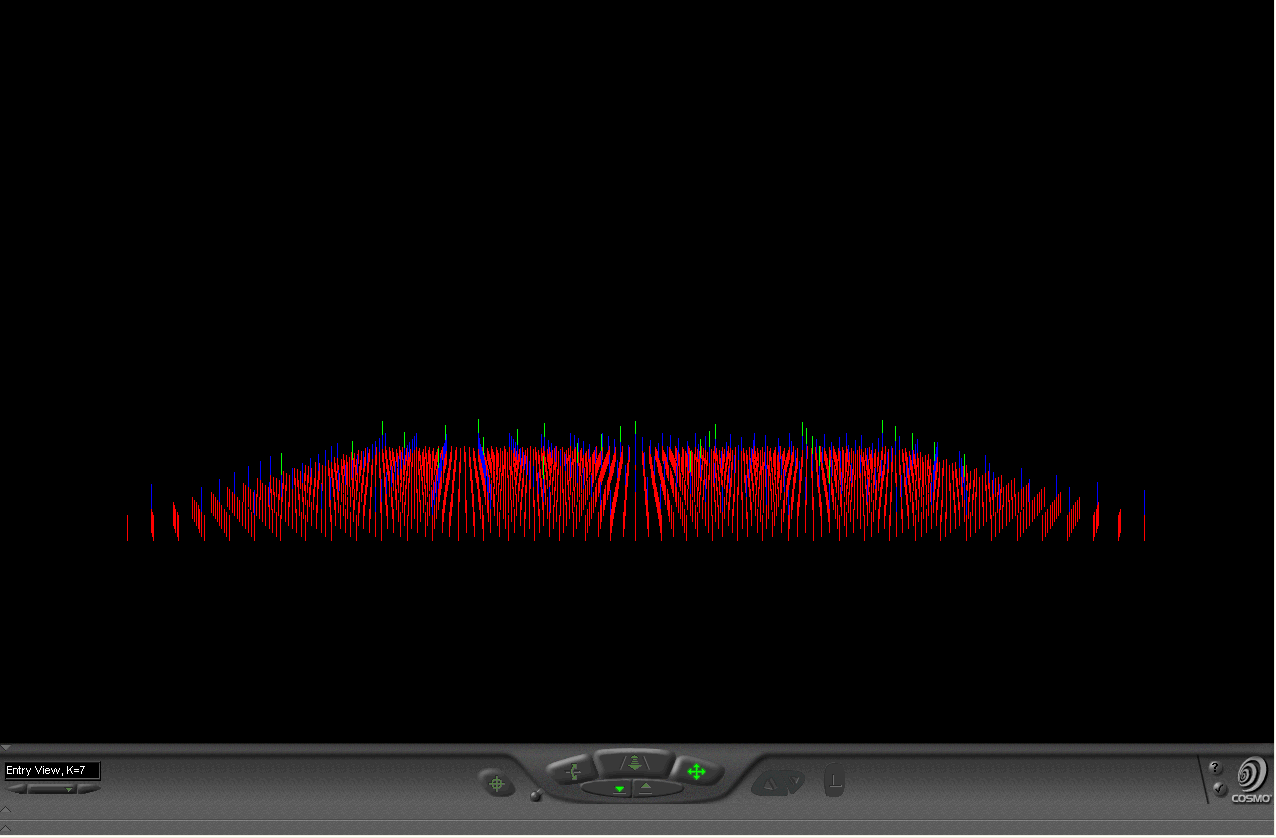
Figure 1.10. K=3, K=4, and K=7 hierarchies animated as viewed from the "entry" viewpoint of associated virtual reality models. |

Figure 1.11. K=3, K=4, and K=7 hierarchies animated as viewed from the "overview" viewpoint of associated virtual reality models. |

Figure 1.12. K=3, K=4, and K=7 hierarchies animated as viewed from the "close up" viewpoint of associated virtual reality models. |
MappletsAnother method, that is available only in current technology, for looking simultaneously at connection patterns between multiple layers of central place networks involves capturing them as Java (TM) Applets: as "Mapplets." This process also suggests some sort of stability of the geometric structure: the mapplet reflects stability in structural form. Shake the mapplet; it settles down to the expected hierarchy. Pull the mapplet; still it settles down to the underlying hierarchical form. One might speculate about real-world forces that pull on mathematical form: the form endures.
Mapplets focus on connection patterns between successive hierarchical layers and, when K values are loaded as distances between hierarchies, they also suggest some elusive form of structural stability of geometric form. Animated maps of the central place geometry of the plane, coupled with mapplets showing animated hierarchical pattern alone, suggest another sort of three dimensional view of central place geometry.
Central place hierarchies as Thiessen polygonsOne difficulty with considering central place landscapes rests in their visualization. Slight errors in placement of points get magnified in overlay alignments. To create a meshed hierarchy in which overlays are aligned is a drafting task of substantial proportions, when done by hand. Geographic Information System software, however, offers an easy and accurate method of constructing central place landscapes at almost any level of complexity (up to the limits of hardware and software capability). Figures 1.4-1.9 were created using ArcView GIS (v. 3.2, ESRI). The method for creating GIS-generated central place landscapes employed the following steps:
Christaller and settlements in Central Europe
The map in Figure 1.16 shows Walter Christaller's sense of regional settlement planning in Eastern Europe. Harris and Berry, note in "Walter Christaller: An Appreciation," that central place theory served as the basis for settlement planning in Eastern Europe:
"...Christaller's involvement in the tumultuous social movements that affected Germany profoundly influenced his life. Like many young Germans, he became aligned with left-wing causes during the 1920s, and later his work was used as the basis of Nazi settlement planning in Eastern Europe. As a result this gentle and kindly man was shunned politically by both East and West after World War II, even as he was being accorded belated recognition for his pioneering contributions to theoretical geography."The first author contacted Harris directly, in writing and on the telephone, to find out more about the source of that statement. The linked letter shows one part of his fascinating answer. He also offers citations to appropriate documents to read. The map in Figure 1.16 is based directly on material from one of these sources.
In it, larger cities are spaced
farther
apart than are smaller ones. Towns and villages fill
interstitial
space. Surely it must have taken Christaller
much time and effort to construct this map. We have
scanned it from
a map in the 1941 reference and pieced together the scanned
images.
The scanning strategy was a multistep process because the map
was quite
large. First, 8.5 by 14 inch photocopies were made of the
map in
the book. It took 8 of those to capture the map, with
overlap.
Then, each piece was scanned at 600dpi on a flatbed
scanner. The
goal was to reassemble the scanned pieces on a canvas in Adobe
Photoshop.
File size of the 8 pieces prohibited such strategy and caused
file oversize
errors. Thus, each piece was reduced in size from 6900
pixels wide
to 2000 pixels wide (preserving the aspect ratio). Then,
each of
these smaller images (smaller in physical size but not in
resolution) was
saved as a transparent .gif. The images with transparent
backgrounds
were then brought into Adobe Photoshop and assembled as a set of
layers;
use of transparency was important because it was only then that
we could
see how to fit the pieces together. To see an even larger
version
of this map (on which place names can be read easily), click here;
the attached file is over 5 MB in size: scroll both
horizontally
and vertically to see the linked map.
 |
Digitize the original map.
One question
that arises is, does the map drawn by Christaller, showing a
plan for settlement
in Eastern Europe, actually conform to a central place theory
pattern as
might be generated today? Preston
(1992) notes that Christaller used an administrative hierarchy,
as well
as a mixed hierarchy, in
creating
plans for the east, mixing marketing, transportation, and
administration/separation
principles. A map of the sort above is complex.
Current technology
permits creation of geometric consideration of historical
evidence.
It is a straightforward manner to digitize the dots set down by
Christaller
in different layers in a GIS according to assigned hierarchical
level.
Use of Thiessen polygons to create pattern is also simple to
execute.
Thus, when the image of Figure 1.16 was brought into Geographic
Information
System software, we separated the layers of dots as Christaller
had suggested
in the legend. The sizes of the colored dots in Figure
1.17 show
an animated view of the seven levels of urban areas entering the
system:
from largest to smallest.
 |
Both the legend of Figure 1.16 and
the
animated map of Figure 1.17 suggest that all layers in this
hierarchy are
similar in nature. A closer look, however, at Figure 1.16
might see
the first five layers as those with central place activities and
see layers
six and seven (the most rural) as working together to form a
single, final
layer that fills in between central places. No sixth or seventh
layer places
have links to subordinate places. Figure 1.18 shows those
two most
rural layers represented as a single layer as a scatter of
yellow dots.
These yellow dots are then analyzed using Thiessen
polygons to create a cellular mesh that appears quite local in
nature.
 |
Figure 1.19 shows a sample overlay
of the
local cellular mesh on the original Christaller map.
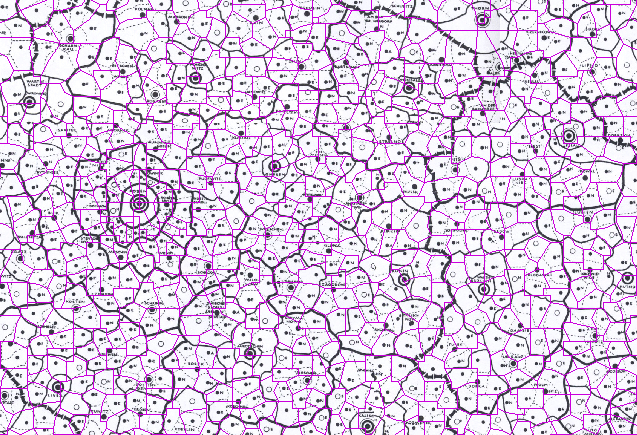 |
Next, we constructed, using the GIS,
Thiessen
central place networks for each of the first five layers of the
hierarchy
identified by Christaller. Figure 1.20 shows these
animated layers
embedded in the convex hull of the map in Figure 1.16.
 |
Figure 1.21 shows a closeup
comparing each
of these layers to the actual map. Note the
underfit/overfit pattern
at the most global level (as with fractal generators for K=7).
 |
 |
When the place names are linked, via
the
hierarchy shown in Christaller's map, as a Mapplet (Figure
1.23), the hierarchical
pattern becomes clear in yet another visual manner.
Figure 1.23.
Clearly one can recreate maps from the past using techniques of the present. The strategy of aligning existing work with new technique will be carried forward into the next chapter. Establishing such alignment is interesting; projecting theorems and concepts on which it is based, into future research, is the real reason for making such alignments: to see that new procedures provide adequate results on known cases so that they serve as a procedural benchmark to extend into new theoretical and practical realms.