Making It Clear: The Importance of Transparency
Sandra Lach Arlinghaus
Klein Earth
| INTRODUCTION Group theory is a branch of mathematics that studies, of course, the structure and behavior of "groups." A mathematical group is composed of a set of elements and a group operation (call it "multiplication" and denote it as *); the set is closed under multiplication--combining elements using multiplication never leads outside the group. It is a closed system. In addition to being closed, a group G with operation *:
Group theory is a highly abstract subject; its abstraction level makes it possible to prove powerful theorems without the clutter of application to obscure thought processes. However, for those wishing to apply the powerful results to other subjects, it may be helpful to visualize the groups geometrically or in some other way. Groups that characterize symmetric structure are often those that are employed elsewhere. For example, W. Pauli employed a particular group of symmetry classes in a physics application associated with particle spin [W. Pauli, 1940]. "In the following
paper we conclude for the relativistically invariant
wave equation for free particles: From postulate (I), according to
which the energy must be positive, the necessity of Fermi-Dirac
statistics for particles with arbitrary half-integral spin; from
postulate (II), according to which observables on different space-time
points with a space-like distance are commutable, the necessity of Einstein-Bose
statistics for particles with arbitrary integral spin. It has been
found useful to divide the quantities which are irreducible against
Lorentz transformations into four symmetry classes which have a
commutable multiplication like +1,-1,+ε,-ε with ε2=1."
|
| CONVENTIONAL
VISUALIZATION OF THE KLEIN FOUR GROUP (VIERGRUPPE) One of the easiest groups to visualize is the one that Pauli used: the Klein Four Group (named for the German mathematician who discovered it, Felix Klein). Often that group is denoted as V4. One way to visualize it is to describe it as the motions of a non-square rectangle. One may flip the rectangle from left to right or from top to bottom. One may also rotate it through 180 degrees. All of these motions leave the position of the rectangle unchanged. Figure 8a-d illustrates the process in four frames. |
 Figure 8a. A rectangle with labelled corners. Motions of the rectangle will be described by change in position of the corners. This configuration of the labels is the base configuration and will be the identity, denoted: (1)(2)(3)(4) meaning that all four corners are fixed. |
 Figure 8b: left-right flip. With respect to the base configuration in Figure 8a, the label 1 goes to where 2 had been and vice-versa. The label 4 goes to where 3 had been and vice-versa. This motion is denoted as (12)(34) meaning that 1 goes to 2 and 2 goes to 1. Also, that 3 goes to 4 and 4 goes to 3. The motion is confined within parentheses. |
 Figure 8c: top-bottom flip. With respect to the base configuration in Figure 8a, the label 1 goes to where 4 had been and vice-versa. The label 2 goes to where 3 had been and vice-versa. This motion is denoted as (14)(23) meaning that 1 goes to 4 and 4 goes to 1. Also, that 2 goes to 3 and 3 goes to 2. The motion is confined within parentheses. |
 Figure 8d: right-left flip and top-bottom flip--rotation through 180 degrees. With respect to the base configuration in Figure 8a, the label 1 goes to where 3 had been and vice-versa. The label 2 goes to where 4 had been and vice-versa. This motion is denoted as (13)(24) meaning that 1 goes to 3 and 3 goes to 1. Also, that 2 goes to 4 and 4 goes to 2. The motion is confined within parentheses. |
| The representation of
these motion using numerals is referred to as a permutation
representation. To combine motions, multiply the
permutations. For example, to multiply the right-left times the
top-bottom motions, multiply their associated permutations as follows. (12)(34) * (14)(23) = (13)(24) where the multiplicative actions is read as: 1 goes to 2 (to the left of the *) and then 2 goes to 3 (to the right of the *) so that all together, 1 goes to 3. That action is then written as (13 . To close the parentheses, start with 3 (to the left of the *): 3 goes to 4 and then 4 goes to 1 so all together, 3 goes to 1. Now, (13) is closed. Then, let's see where 2 goes. Start with 2 to the left of the * where 2 goes to 1. To the right of the star, 1 goes to 4, so all together 2 goes to 4. Check also that 4 goes to 2: 4 goes to 3 (to the left of the *) and 3 goes to 2 (to the right of the *) so all together 4 goes to 2. Thus, we have (24). The final result of the multiplication is (13)(24). |
| Figure 9 shows a
multiplication table for all four of these
motions. It shows that the system is closed under the operation
of *. There is an identity element; each element has an inverse;
and the associative law holds. Thus, this system is a
group. It is also a commutative group: note the symmetry
about the main diagonal. It is this group that is known as the
Klein Four Group. |
||||
| * |
(1)(2)(3)(4) | (12)(34) | (14)(23) | (13)(24) |
| (1)(2)(3)(4) |
(1)(2)(3)(4) | (12)(34) | (14)(23) | (13)(24) |
| (12)(34) |
(12)(34) | (1)(2)(3)(4) | (13)(24) | (14)(23) |
| (14)(23) |
(14)(23) | (13)(24) |
(1)(2)(3)(4) | (12)(34) |
| (13)(24) |
(13)(24) | (14)(23) | (12)(34) |
(1)(2)(3)(4) |
| Figure
9. Permutation representation of the Klein Four Group:
multiplication table. Multiplication takes place as entry from
left-hand column times entry from top row. |
||||
| GOOGLE GLOBE
INTERPRETATIONS The interpretation of this group as the motions of a rectangle suggests, perhaps, further visualization of it on a sphere. When that sphere is the globe, with north and south poles, then the idea is that there is and East-West flip and a North-South flip, as well as rotation through 180 degrees. It is a simple matter to put a rectangle on the transparent Google globe. Figure 10 shows the rectangle from Figure 8a superimposed on the Google globe. Naturally, one could then superimpose the remaining rectangles but that would be of little interest. Far more interesting is to see what motions of the globe, when applied only to Figure 8a, will produce the other elements of the Klein Four Group. Figures 10a-d show the motions of the transparent Google globe that will produce the Klein Four Group using the rectangle from above embedded on the globe's surface. |
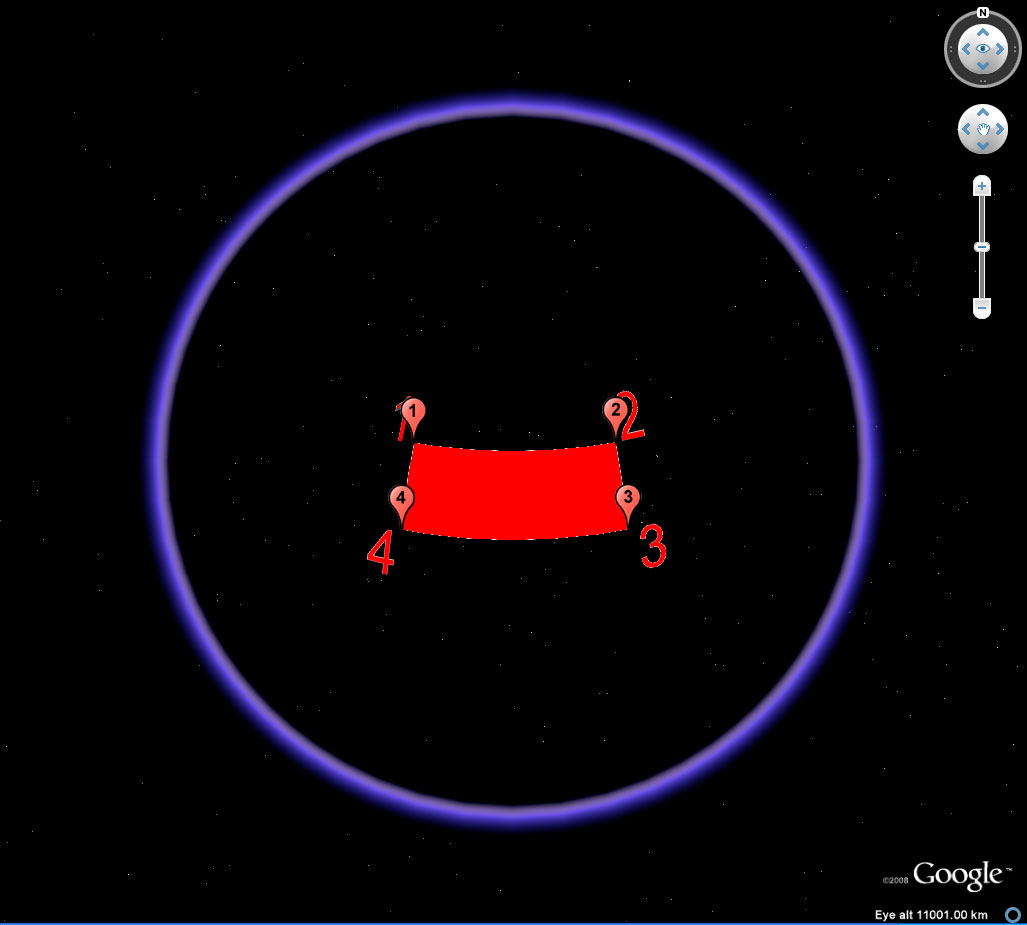 Figure 10a. The identity position shown on the part of the globe facing the reader. The placemark balloons show up only on the "front" of the globe. Associated kml file applies to all frames of this figure. |
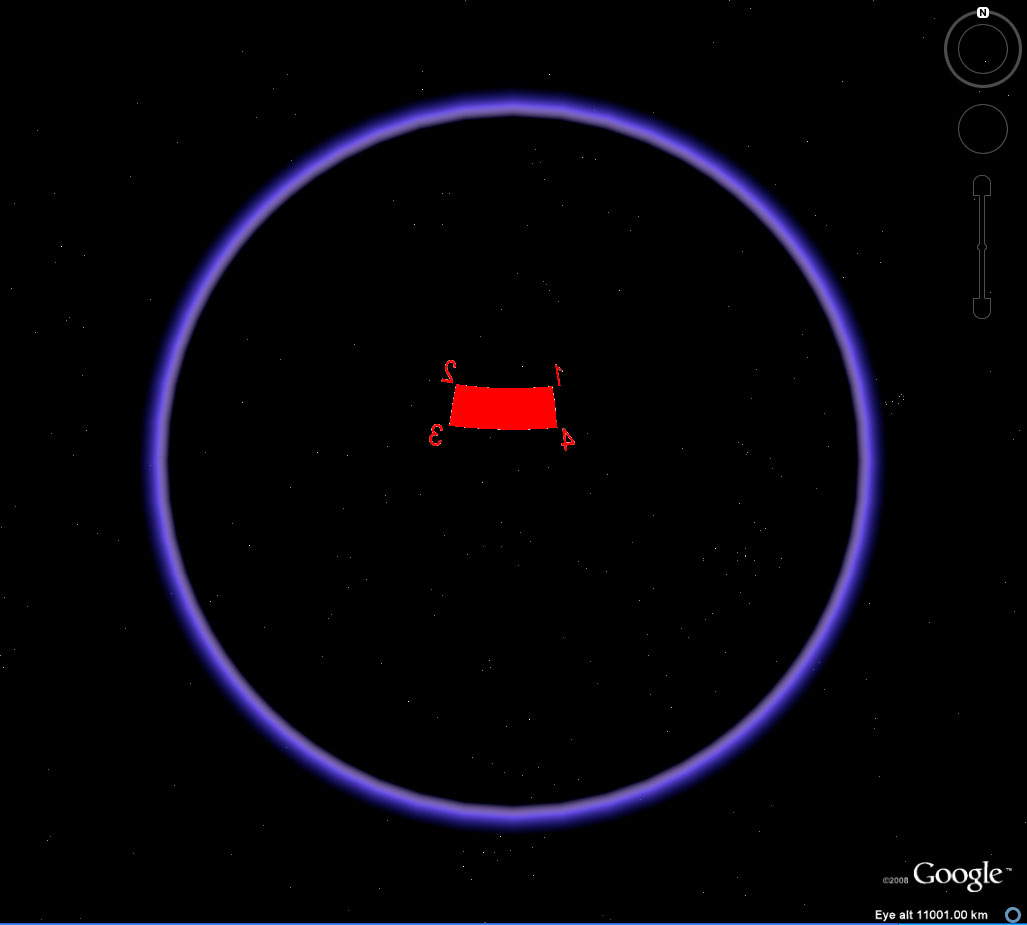 Figure 10b. The EW flip position emerges on the back of the globe when the globe is spun to move the rectangle from 10a to the back. Notice that the placemark balloons no longer show even though they are turned on. |
 Figure 10c. The top-bottom, or NS flip. Notice that the orientation dial in the upper right corner as now been rotated to the south position. Thus, this NS flip is a product of the EW flip and rotation permutations--as in the Table of Figure 9. Again, the placemark balloons show up only on the "front" of the globe. |
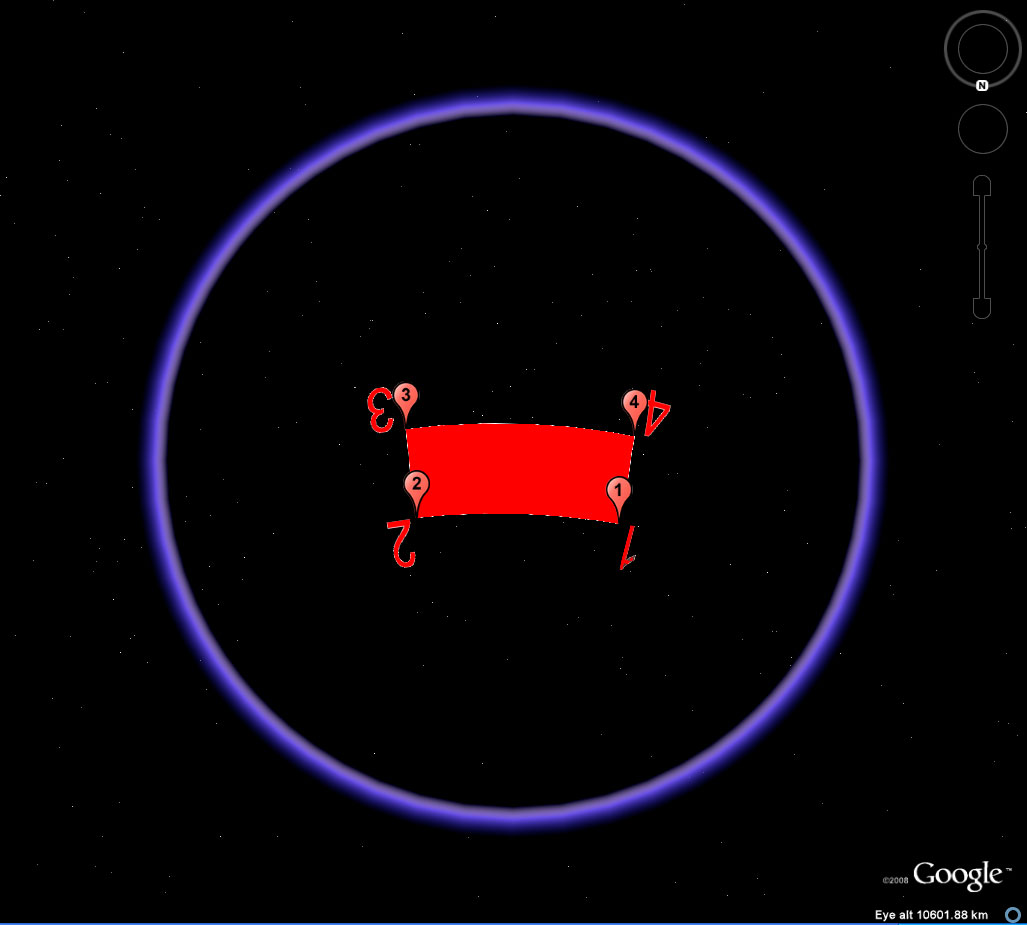 Figure 10d. The rotation position shown on the part of the globe facing the reader. The placemark balloons show up only on the "front" of the globe. |
| When the rectangle is expanded so that the four vertices lie along a great circle as the joining rectangle (Figure 11), then one might consider the Klein Four group in association with various global transformations. |
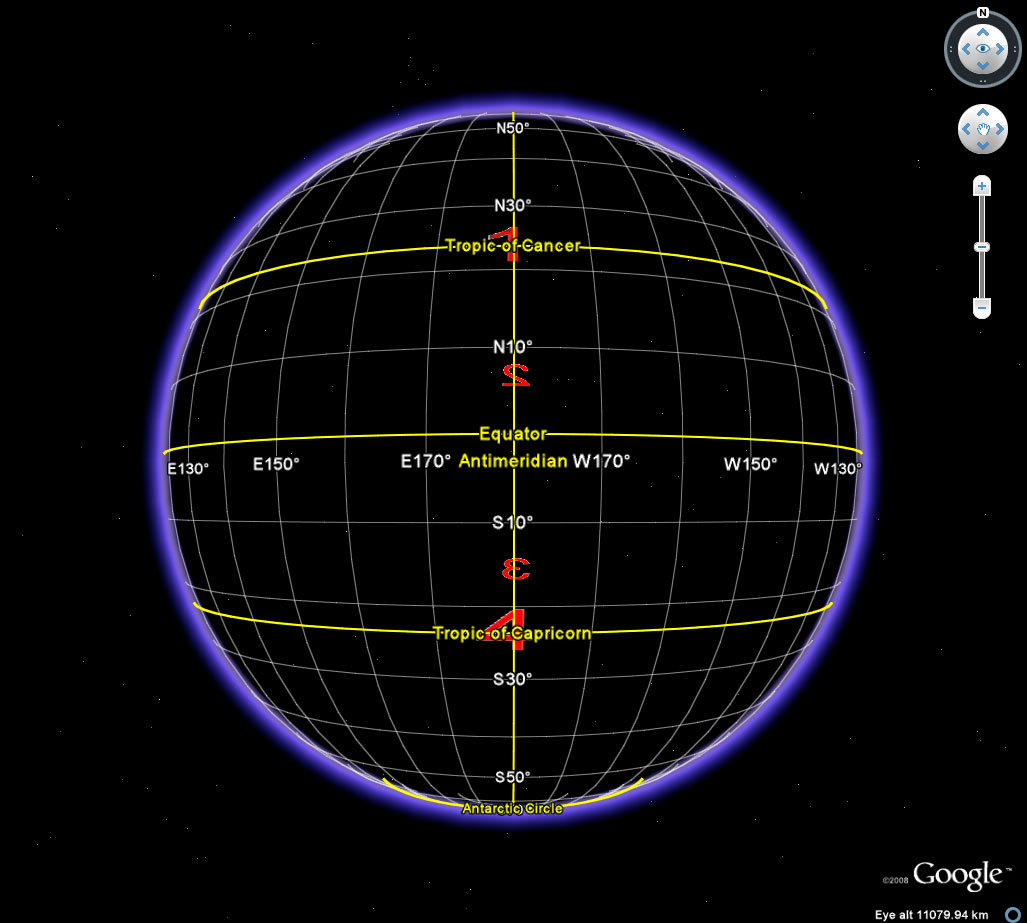 Figure 11. The four vertices of a rectangle lie along a single great circle. The rectangle is centrally symmetric. |
| Figure 12 displays the positions of the four vertices in various positions on the transparent globe. Vertices in back have labels that are smaller than those in front. Spinning the globe in various directions, with some vertices in front and some in back, creates the pattern of the four vertices, when visualized as "flat", that arise in the motions of the rectangle in the plane. Other than overlapping labels or superimposed vertices (which change with vantage point), it is those Klein positions, and only those, that arise from any rotation of the sphere. Placement of a single labelled rectangle on the sphere generates all Klein positions and no other non-trivial ones. |
 Figure 12a. Largest rectangle embedded on the surface of the Google Globe. Identity position. Associated .kml file applies to all frames of this figure. |
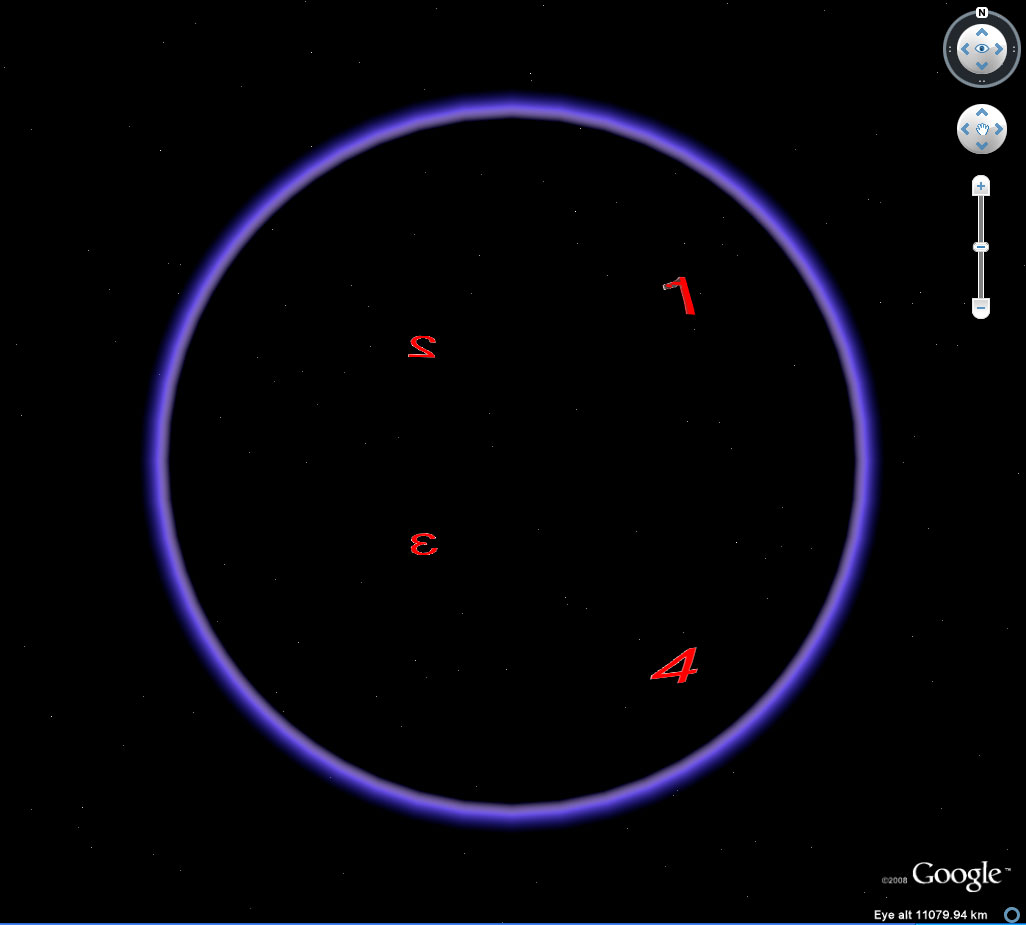 Figure 12b. Largest rectangle embedded on the surface of the Google Globe. East-west flip. |
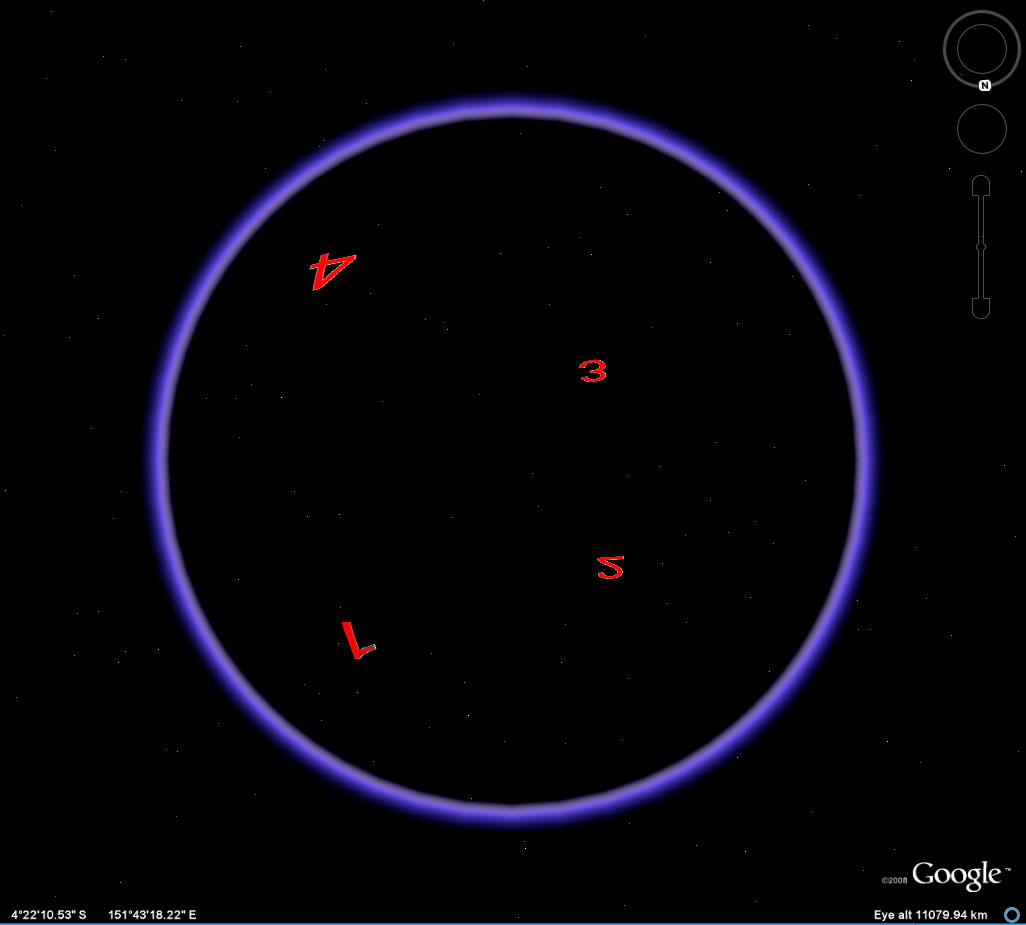 Figure 12c. Largest rectangle embedded on the surface of the Google Globe. North-South flip. |
 Figure 12d. Largest rectangle embedded on the surface of the Google Globe. Rotation of 180 degrees. |
| The
Kleinian view of the globe, expressed in the theorem below, is the
fundamental theorem of
the abstract structure of the Earth-Sun system. Perhaps it is not
surprising that the same four symmetry classes that were found to
characterize particle spin more than half a century ago also
characterize, in some sense, the larger "particle" on which we live. Theorem: When this set of transformations, forming the Klein Four Group of a centrally symmetric rectangle inscribed in a great circle through the poles of the Google Globe (Figures 12a-12d), is interpreted in the context of Earth-Sun relations,
|
| Corollary:
The rotational transformation is a Möbius
strip transformation. To glue antipodal points 1 and 3 together
in the rotational transformation give one end of the identity rectangle
a twist and bing the 23 edge over to the 14 edge aligning 1 and 3; and,
2 and 4. A Möbius strip is
created. Tobler (1961) noted one way to map the world on a Möbius strip. That method did not display the full globe. Later, Arlinghaus (1985) created the full map using the strategy noted above. It served as a base for making calculations in the world of art (Arlinghaus and Nystuen, 1986). |
| Corollary:
The East West flip is identical to the view of the
Earth from inside the globe (Figures 13a-c). Thus star charts are terrestrial maps subjected to one element of the Klein Four Group. |
 Figure 13a. The vertices 1 and 4 lie on the Antimeridian (180 degrees longitude) while the vertices 2 and 3 lie on the Meridian (0 degrees longitude). Here the view of the globe is from the outside. |
 Figure 13b. Inside out. The vertices 1 and 4 lie on the Meridian (0 degrees longitude corresponds to 00h right ascension). East and west are flipped by using the "sky and earth" switch in recent versions of Google Earth. |
 Figure 13c. Inside out. The vertices 2 and 3 lie on the Antimeridian (180 degrees longitude corresponds to 12h right ascension). East and west are flipped by using the "sky and earth" switch in recent versions of Google Earth. |
REFERENCES:
- Arlinghaus,
Sandra L. Antipodal graphs. Abstract #3792-92-404, Abstracts of the American Mathematical
Society, Vol. 3, No. 1, 1985.
- Arlinghaus,
Sandra L. and Nystuen, John D. Sandra
L. Mathematical
Geography and
Global
Art: the Mathematics of David Barr's `Four Corners Project'. Institute of Mathematical Geography. 1986. Monograph
One
- Mandelbrot, Benoit. The Fractal Geometry of Nature. New York: W. H. Freeman, 1982.
- Mozart,
Wolfgang. Eine Kleine
Nachtmusik. Link.
- Pauli, W. The Connection Between Spin and Statistics, Phys. Rev. Vol. 58, Issue 8, 716 - 722 (1940)
- Tobler, W. "World map on a Moebious strip," Surveying and Mapping, XXI, 4 (1961), p. 486.
- Vivaldi,
Antonio. Excerpt--Spring,
The Four Seasons. Herbert Von Karajan and Anne-Sophie Mutter,
Berlin. Winter,
Largo: Itzhak Perlman
- Others inline,
as citations or as suitable music, or
archived in Deep Blue.
Dr. Arlinghaus is Adjunct Professor at The University of Michigan, Director of IMaGe, and Executive Member, Community Systems Foundation.
Solstice: An Electronic Journal
of Geography and
Mathematics,
Institute of Mathematical Geography, Ann Arbor, Michigan.
Volume XIX, Number 2.
http://www.InstituteOfMathematicalGeography.org/
Persistent URL: http://deepblue.lib.umich.edu/handle/2027.42/58219
Volume XIX, Number 2.
http://www.InstituteOfMathematicalGeography.org/
Persistent URL: http://deepblue.lib.umich.edu/handle/2027.42/58219