Spatial Synthesis:  Volume II, Book 2.
Making It Clear:  The Importance of Transparency

Sandra Lach Arlinghaus

Fractal Earth
Download  this associated kml file for the first section.


SECTION 1:  SELF-ECLIPSING TILES ON THE GLOBE
In the chapter on Escher/Barr Earth, it was noted that polygons on the surface experience a "self-eclipsing" effect when they are spun around the globe, as they move from front to back.  The extent to which the eclipsing effect occurs appears to depend  on where they make the front to back transition.  In Figure 1, the Koch Island, a classical fractal curve, is shown at a fairly simple state of fractal iteration.  Three copies of that curve are stacked up at 50,000 meters (yellow), 100,000 meters (red), and 150,000 meters (purple).  They are stacked on a white base tile that is clamped to the ground on the Google Globe (with the terrain switched off).  The figure is animated to show the effect of moving this stacked Koch tile in a due east-west direction.

Figure 1.  Animation of an East-West tour of a Koch Island tile (low in the fractal iteration sequence).  Download the associated kml file and play the EW tour or move the tile around freely to study self-eclipsing effects as the tile moves from front to back of the Google Globe.


Figures 2a, 2b, and 2c show Koch Island tours (Koch's Tours?) along great circle routes at headings of 45 degrees, 67 degrees, and 90 degrees respectively.  The interval between successive screen shots in the animation is 20 degrees of longitude.  The images in Figure 1 and Figure 2 all suggest that the self-eclipsing effect is strong near the horizon, only. 

They also suggest that there may be variation, depending on heading, as to when the white base comes into view on the back side.  There is a region of "umbra" in which the non-white stack is visible near the edge but none of the white is visible.  There is a region of "penumbra" in which only part of the white base is visible.   Once the stack is beyond the penumbra on the backside, a sort of Moiré effect from the translucent tile reveals the underlying graticule on which the projection is based. 

The projection appears to be an orthographic projection:  a perspective projection from sphere to plane in which the center of projection is from a point at infinity.  The center of the Koch Island tile in initial position, and its antipodal point, form a central axis for these views of the circulating tiles independent of heading.  

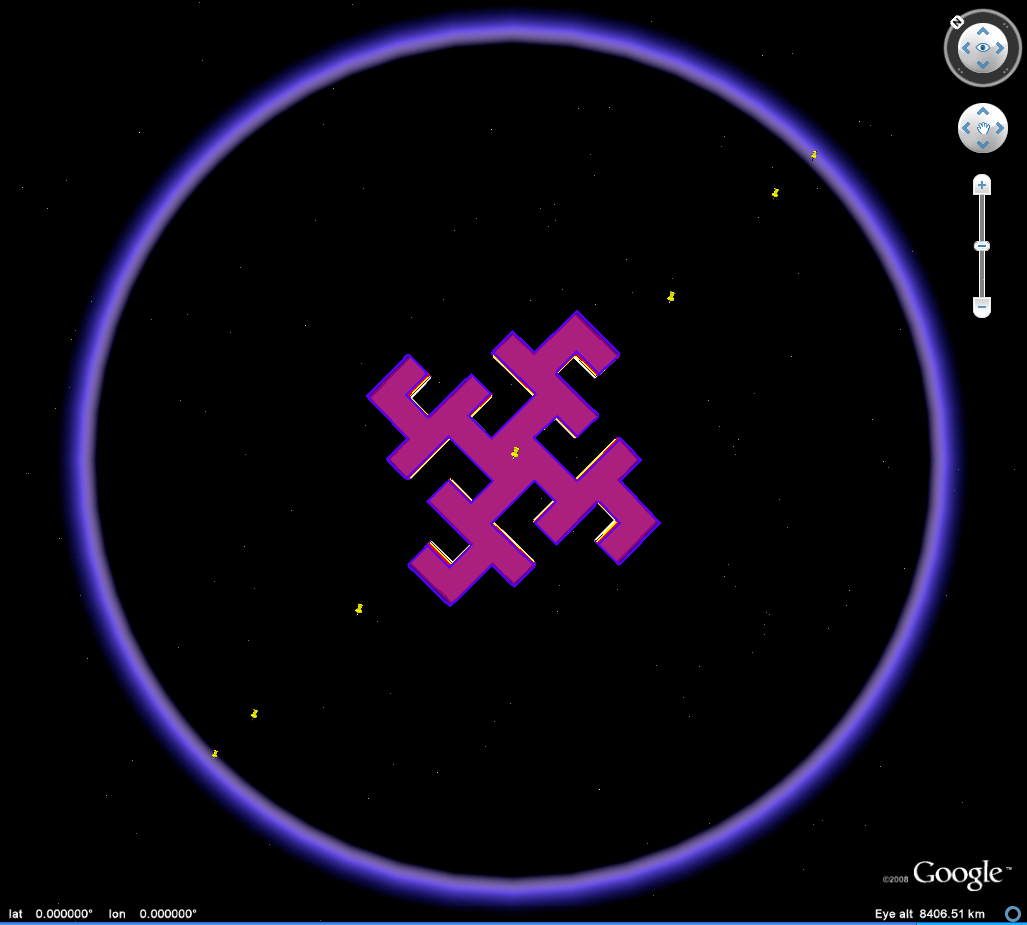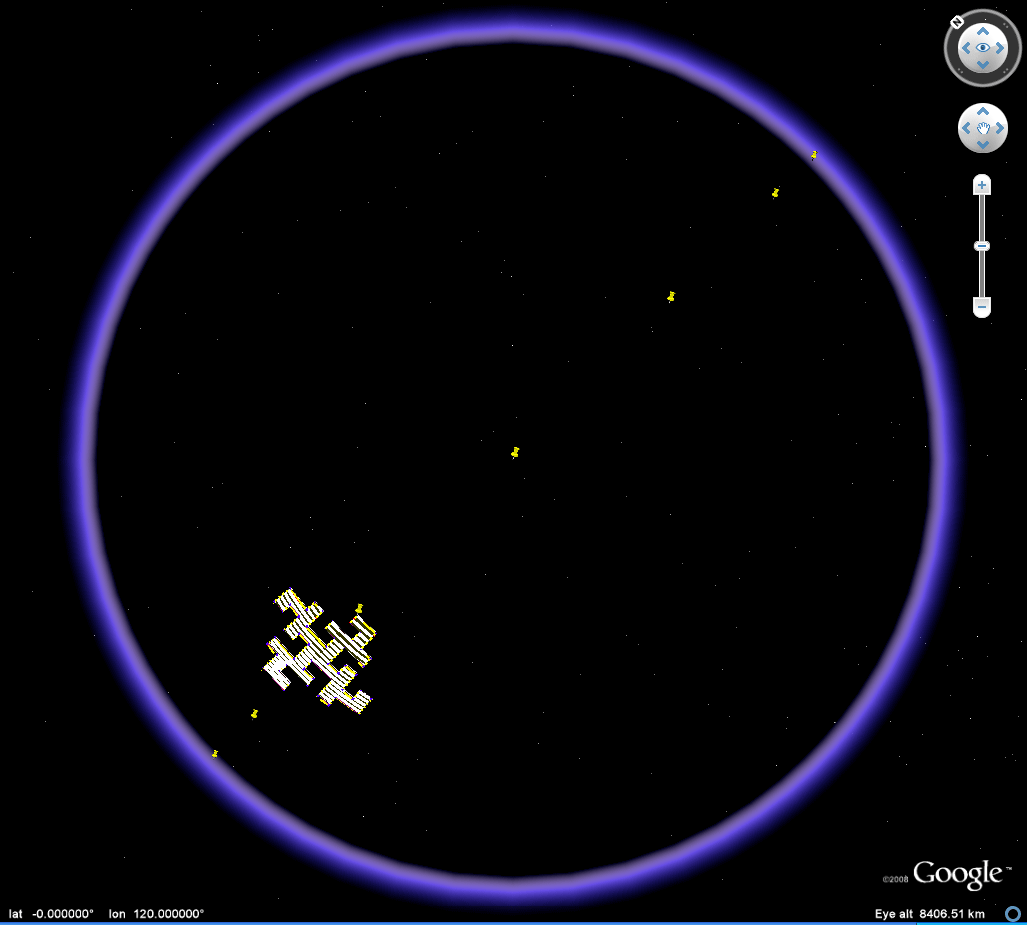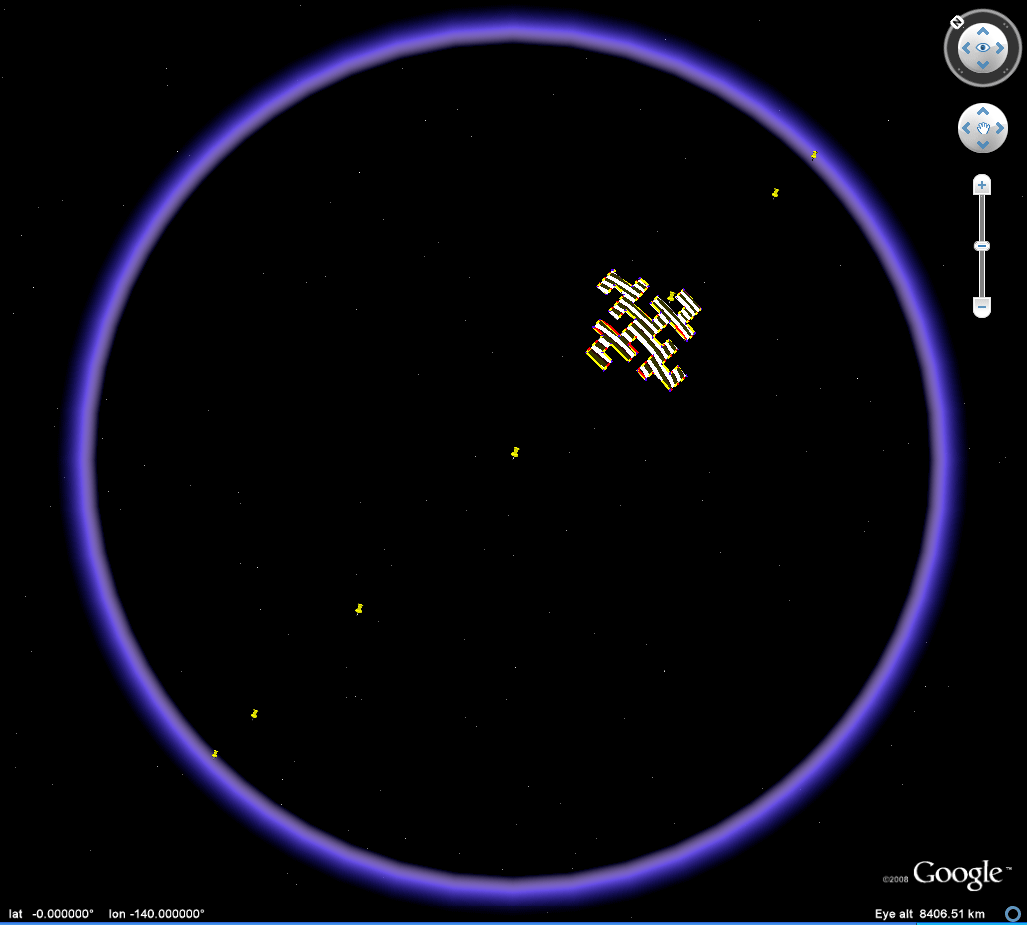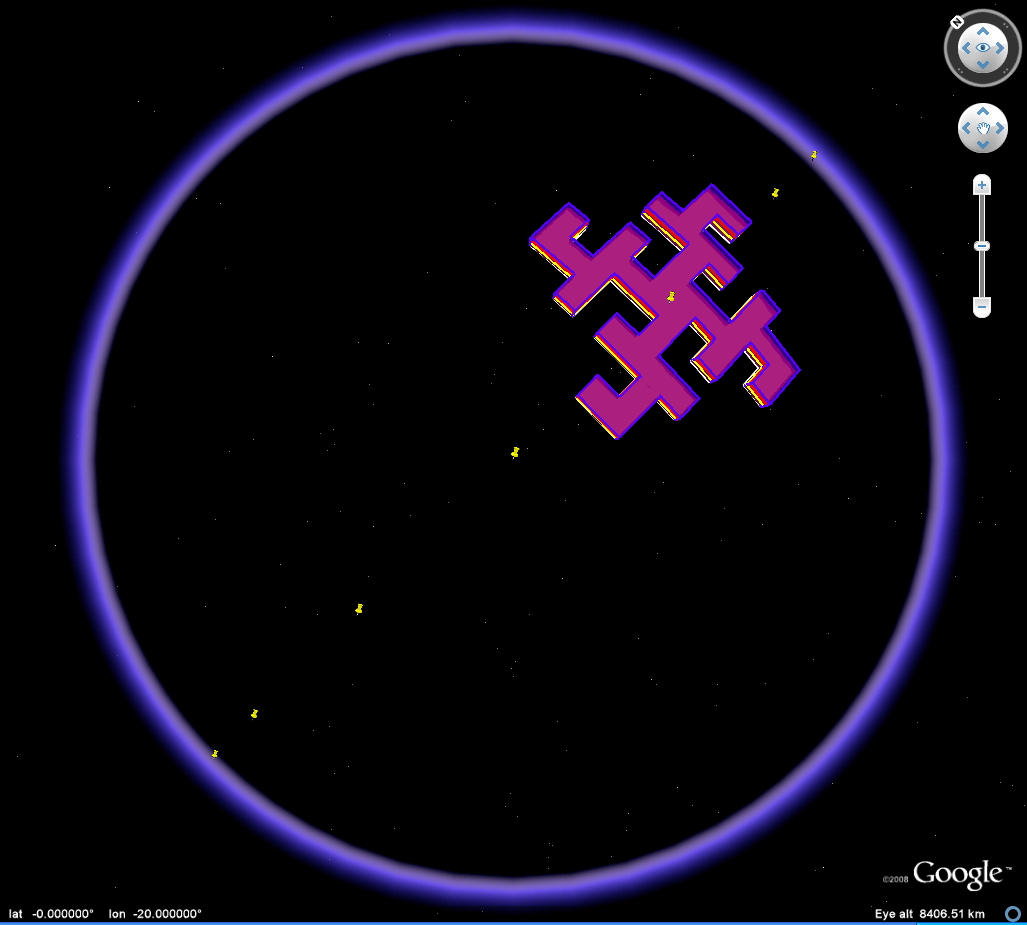Figure 2a.  Animation of an 45 degree heading great circle tour of a Koch Island tile (low iteration).  Download the associated kml file and play the 45 degree tour or move the tile around freely to study self-eclipsing effects as the tile moves from front to back of the Google Globe.

Figure 2a.  Animation of a 67 degree heading great circle tour of a Koch Island tile (low iteration).  Download the associated kml file and play the 67 degree tour or move the tile around freely to study self-eclipsing effects as the tile moves from front to back of the Google Globe.

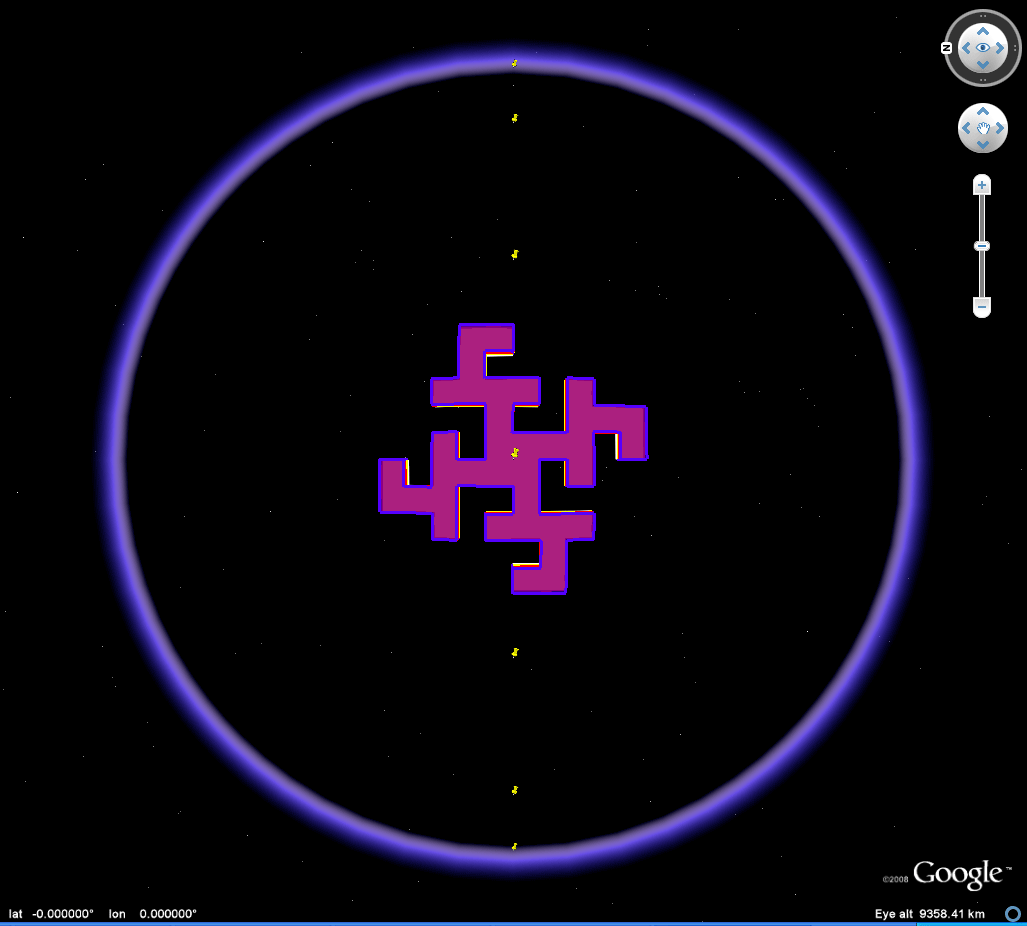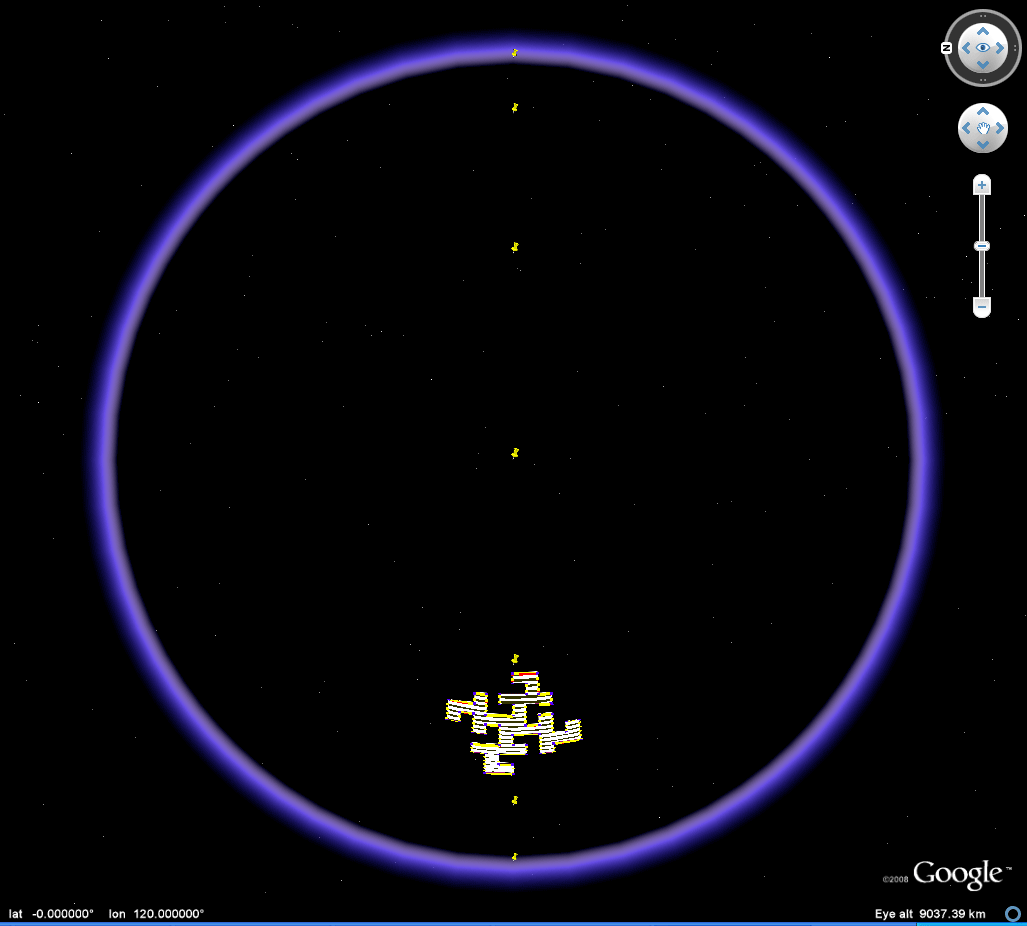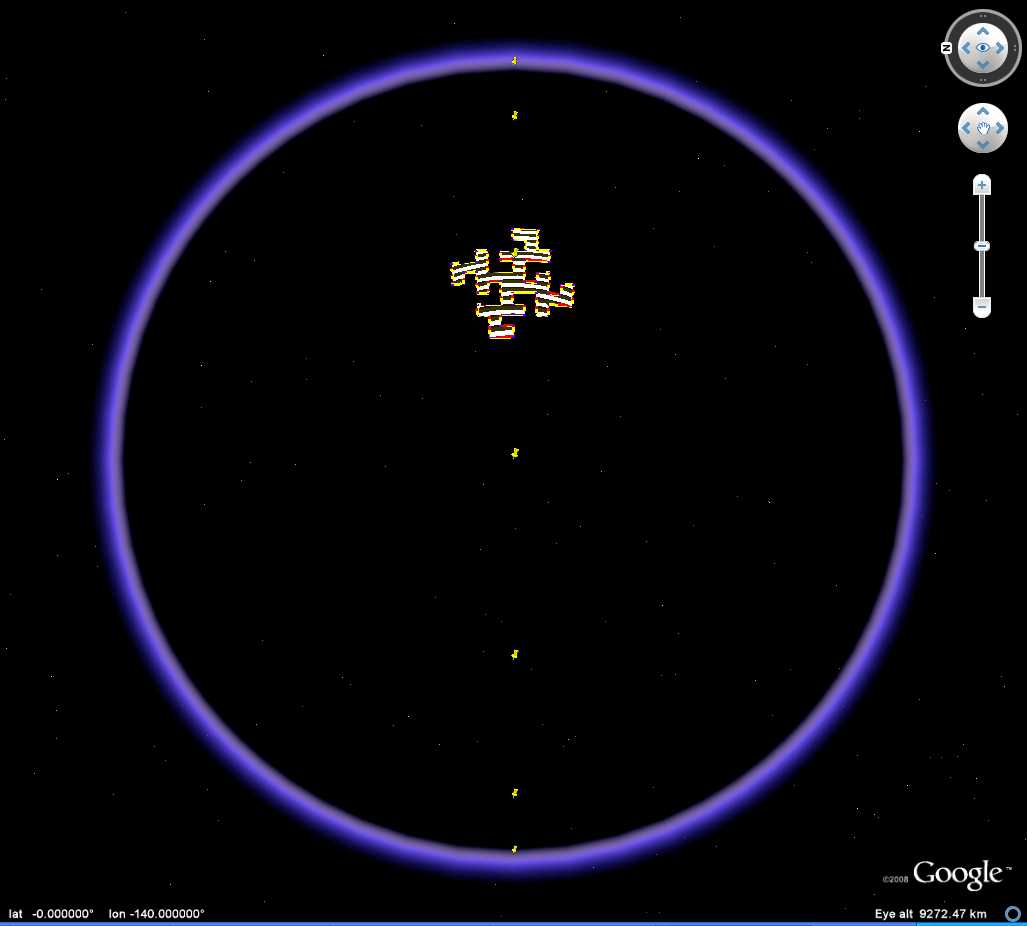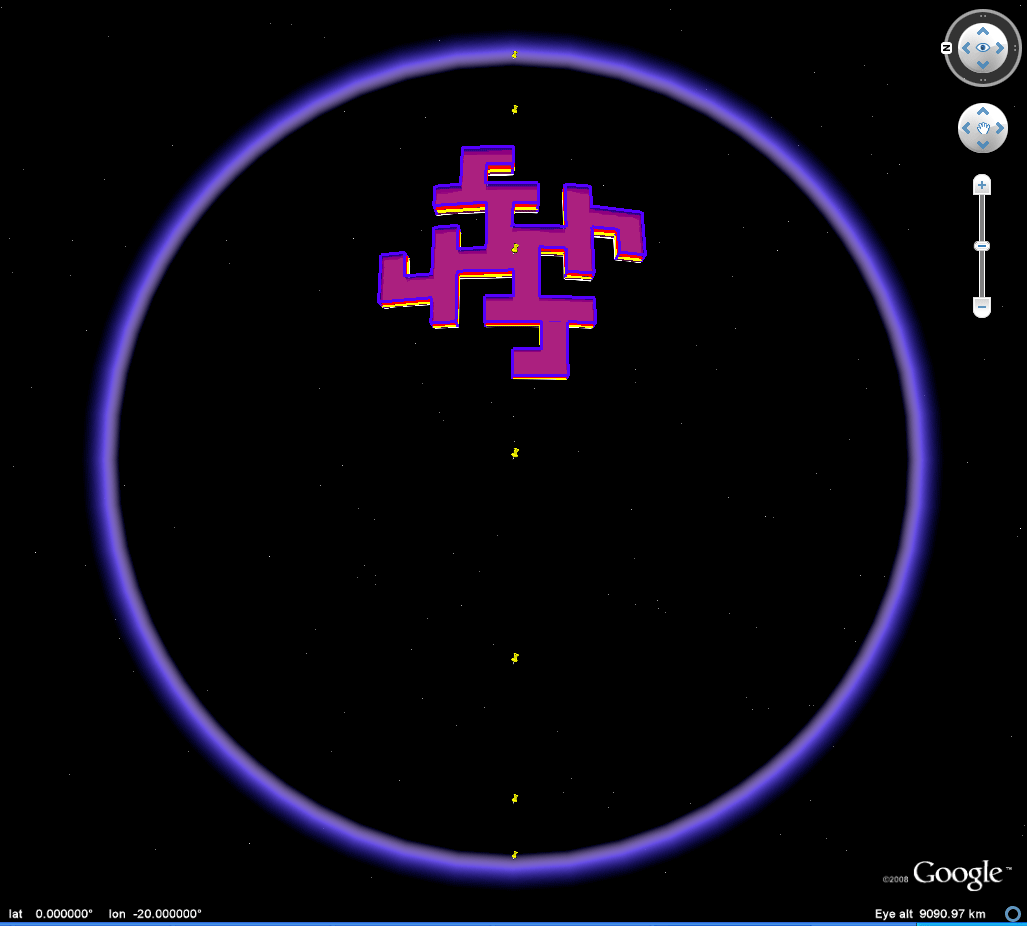Figure 2c.  Animation of an 90 degree heading great circle tour of a Koch Island tile (low iteration).  Download the associated kml file and play the 90 degree tour or move the tile around freely to study self-eclipsing effects as the tile moves from front to back of the Google Globe.



A simple shot of the Grid, from a polar perspective (Figure 3) shows the characteristic spacing of the orthographic graticule with great circles becoming more closely spaced as one moves away from the center (which is assumed along the Earth's polar axis--conversation wtih Michael Weiss-Malik at lunch (October 23, 2008) in which he noted that the Google Earth singularities are at the Earth's poles).  Thus, zoom length can be "infinite."  The map "looks" like the globe.   The central-axis property revealed by the Moiré effect on the tiles in Figures 1 and 2 is clearly the case for all headings, and not just those tested, if the underlying projection is indeed orthograpic.  

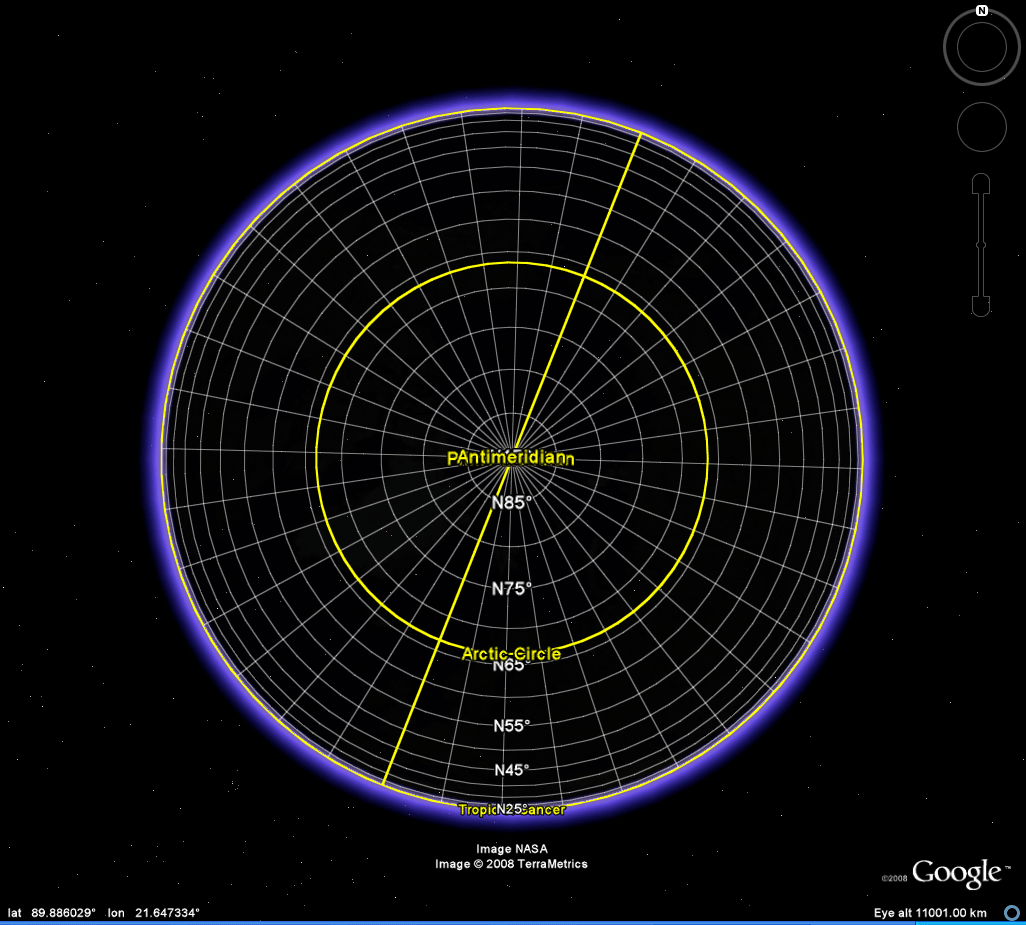Figure 3.  Apparent orthographic graticule serving as the projection base for the Google Globe.



When the vantage point is varied the location of the umbra and penumbra will vary.  Consider the images in Figure 4:  they show views of the Koch Island tile all at 110 degrees East Longitude at varying values of Latitude (10, 20, 30, 40, 50, 60, 70, 80, 89).  The white base of the tile comes into view at variable positions.  One might speculate that perhaps the crossing of a singular point is the cause:  the software produces errors when trying to enter (110, 90).   Or one might be tempted to think that the crossing of tiles of the underlying quadtree data structure alters the location of the umbra and penumbra.  There are experiments, suitably named, also in the kml file for download.  Those reasons, while perhaps natural concerns, appear not to have much merit. 

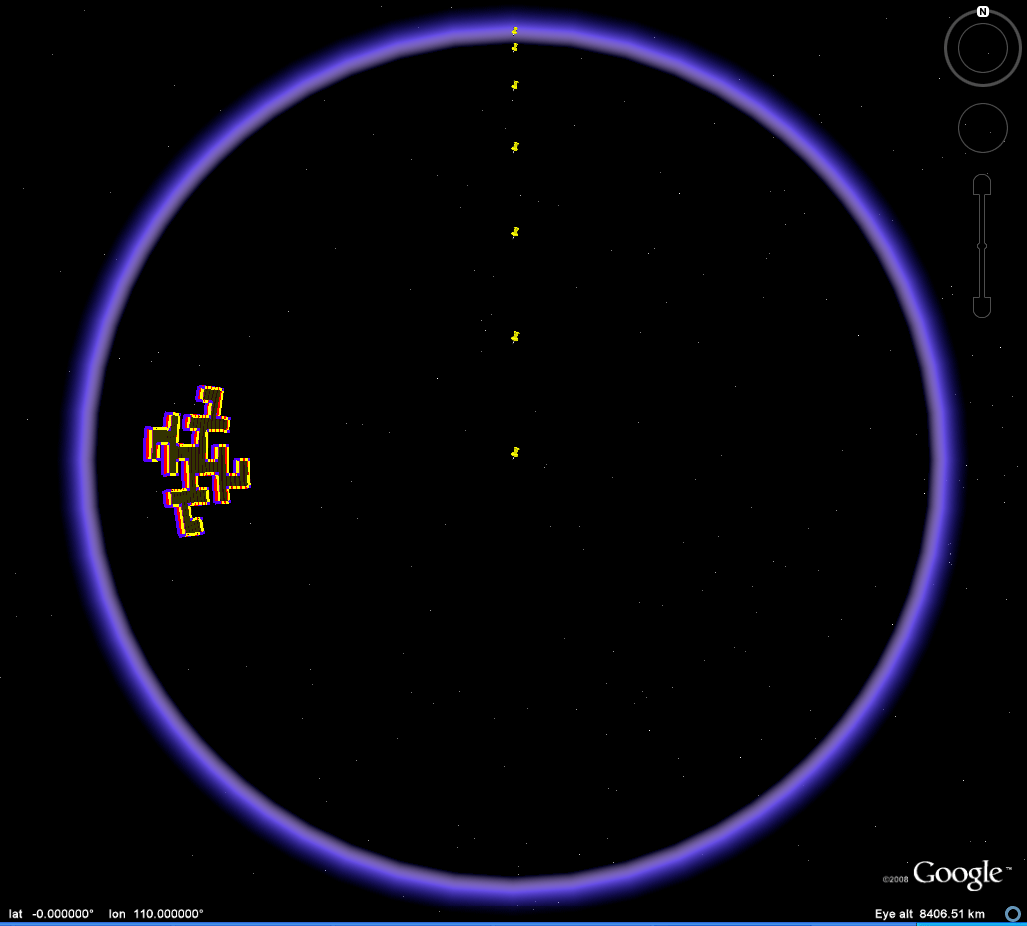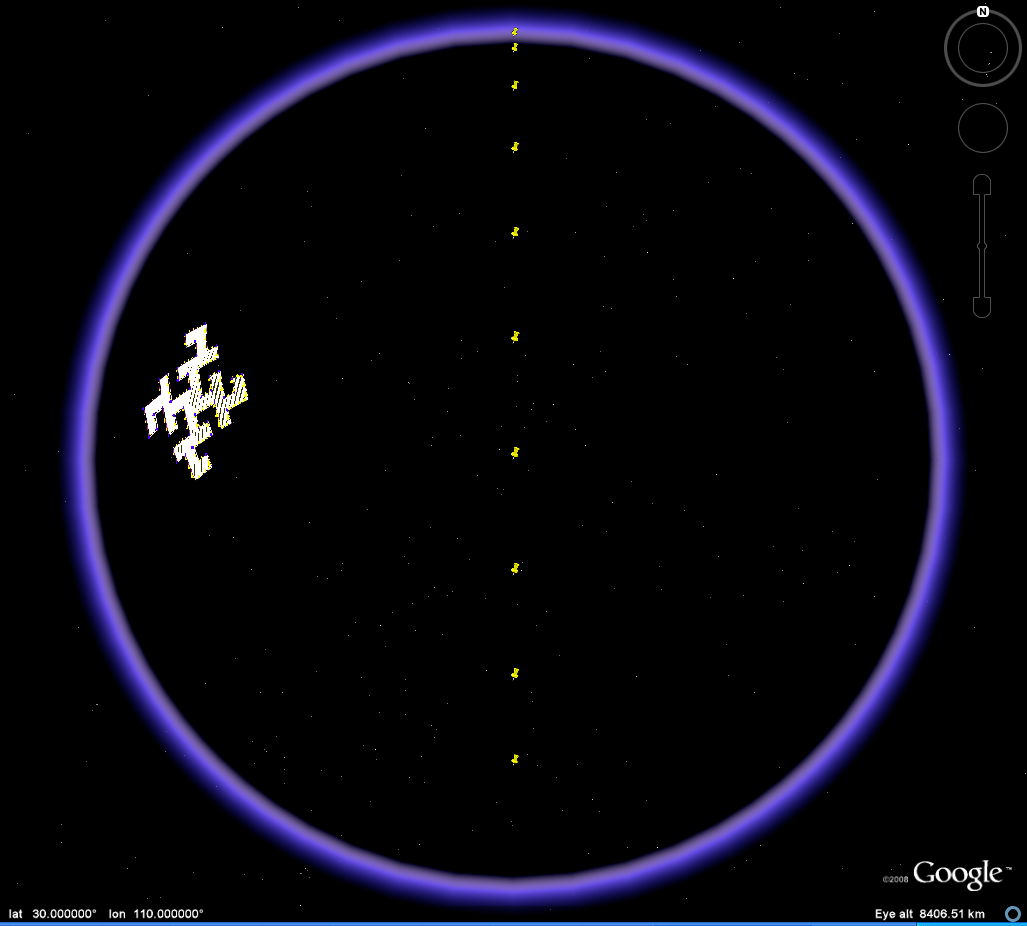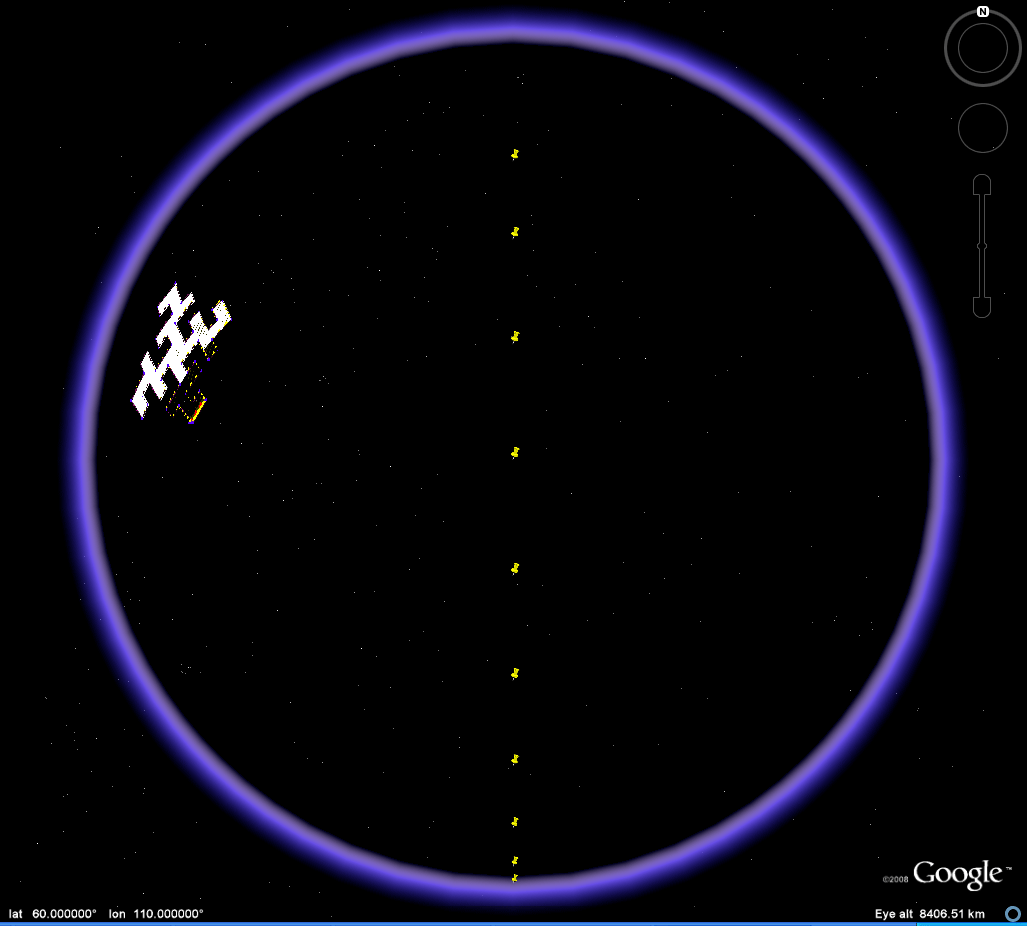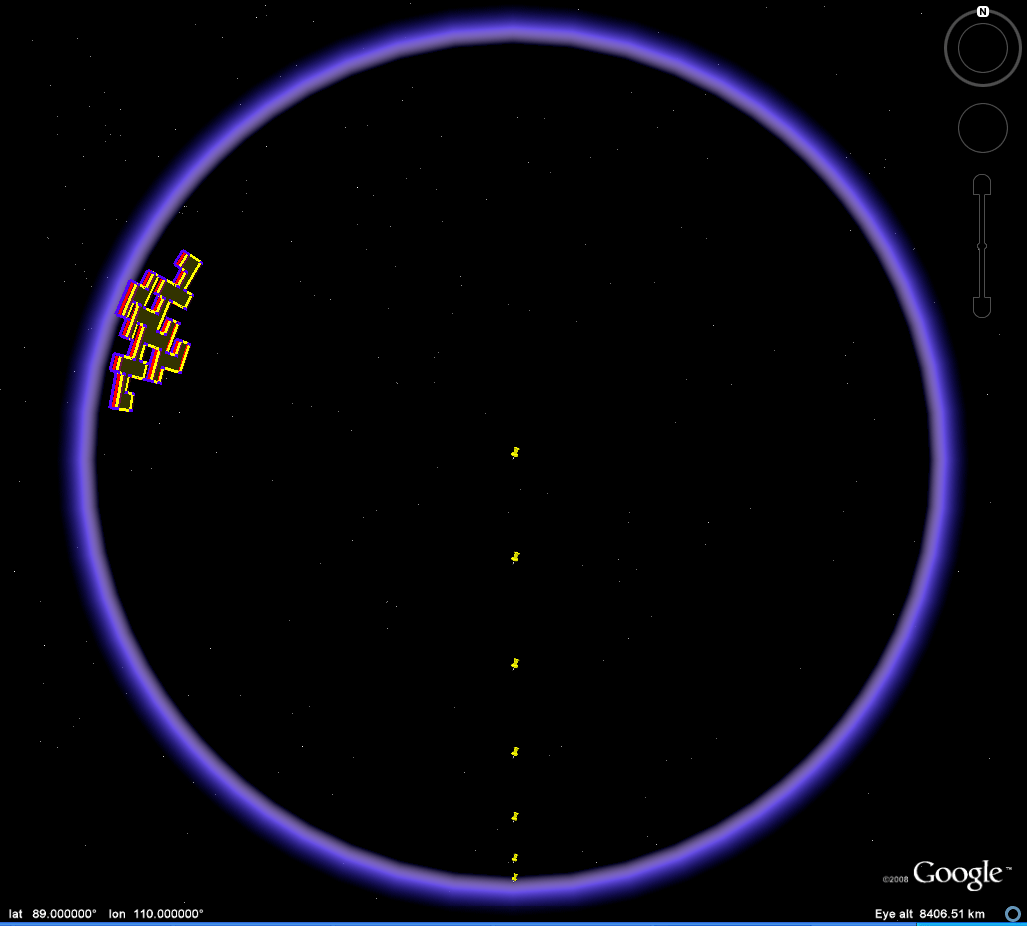Figure 4.  Koch Island tiles along the horizon.



What matters is primarily the position of the observer:  much as it does in a solar or lunar eclipse.  Figure 5a shows the position for (50,110) from the animation above.  Figure 5b shows the same tile, in the same position, viewed from the North pole.  Because this latter vantage point is along the axis of the underlying orthographic projection, there is no variation, of the sort in Figure 4, in position of umbra and penumbra.   Use the kml file to have multiple views and to see this effect clearly for any location.  

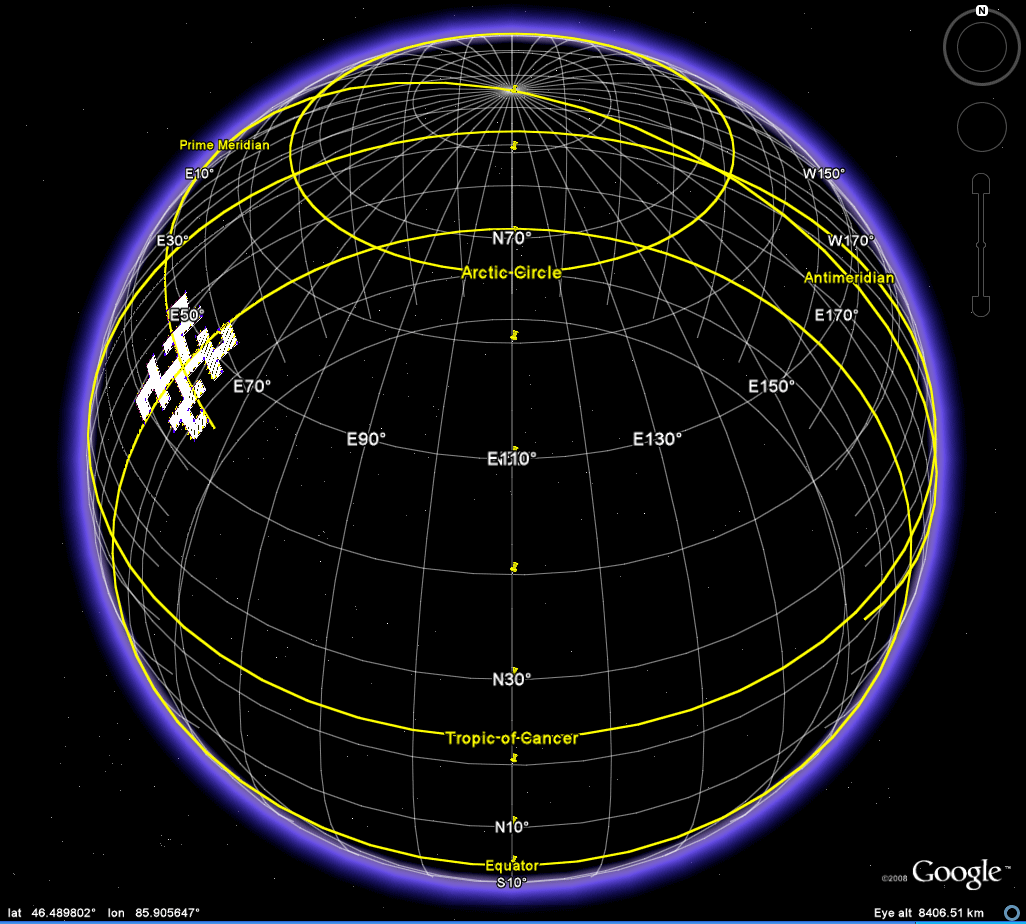Figure 5a.    Lateral view of the Koch Island tile located at (50, 110).

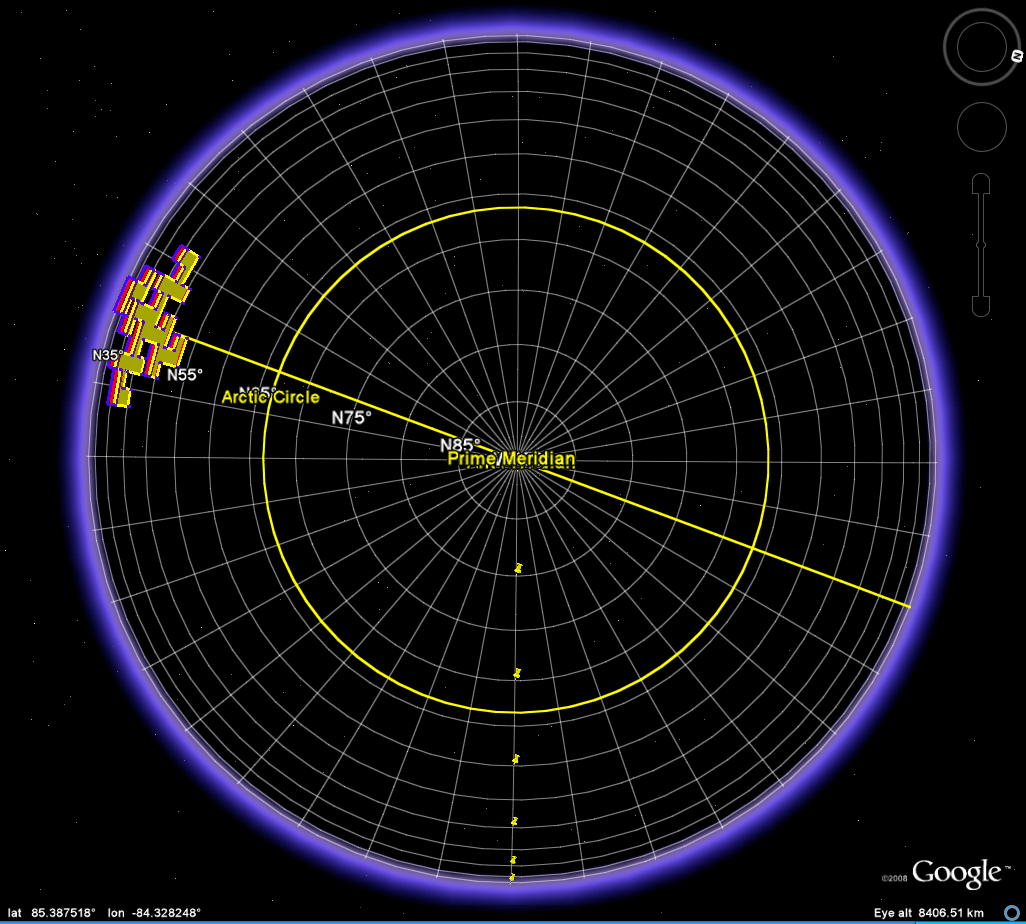Figure 5b.   Polar view of the Koch Island tile located at (50, 110).

Questions for further thought:
  • The spacing of layers in the Koch Island tile was linear; what might the Moiré effects be like in a non-linear spacing pattern?  What might they suggest?  Classification according to type:  Logarithmic, exponential, and so forth?
  • Self-eclipsing, as a concept--might it lead, especially using considerations in the bullet-point above, to some sort useful visualization of geometric objects much as computer visualization did for the concept of self-similarity as a "fractal"?
  • Projection changes:
    • The interior of the Google Globe appears to have a gnomonic graticule.  What implications are there for the ideas above in regard to that?
    • Inverse stereographic projection makes the non-compact plane into a compact sphere by adding one point (at a pole, for example) according to the Alexandroff One-Point Compactification Theorem.  Again, what implications might there be for self-eclipsing tiles with respect to that idea?
    • Same questions for the infinity of projections available.
The study of  these conceptual experiments not only provides insight into the geometry of Google Earth but it also offers insight into eclipses in general.   Visualization on the entire sphere, which requires transparency, is important in diverse fields of endeavor.


SECTION 2:  SELF-SIMILAR TILES ON THE GLOBE-- A HEXTREE BASIS?


Apparently, the quadtree (or perhaps octree?) is the basis for the data structure underlying Google Earth (Mano Marks, workshop communication, October 23, 2008).  A visual representation of these structures has a fractal-like form in which the same pattern is applied to partition data at successively more local scales. 

Broadly viewed, one might then wonder if some sort of geometry configuration, based on close-packings, might be an interesting way to split up tiles on the surface of the sphere.  Hexagons form the tightest close-packing.  A number of years ago, Azriel Rosenfeld noted, at an American Mathematical Society meeting, that hexagonal pixels would make sense if one were trying to optimize spatial content on a computer screen.  He noted, however, that printer technology was based on a rectilinear grid and so the requirements for a skewed-looking printer were not appealing to printer manufacturers. 

Later essays (see references) note various uses and theoretical findings involving hexagonal packings.  Figures 6a, 6b, and 6c, show three different close packings with layers of successively smaller polygon nets oriented in a variety of patterns--they determine, in a general sense, all others.  Each may be fractally generated and each is listed with its fractal dimension (space-filling capability).

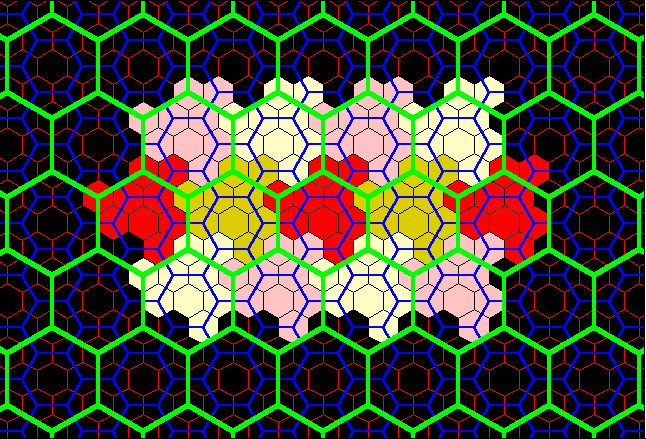Figure 6a.  Principle of 3.  Fractal generation procedure suggested by tiling pattern.  Fractal dimension when iteration is carried out infinitley is:  1.2618595

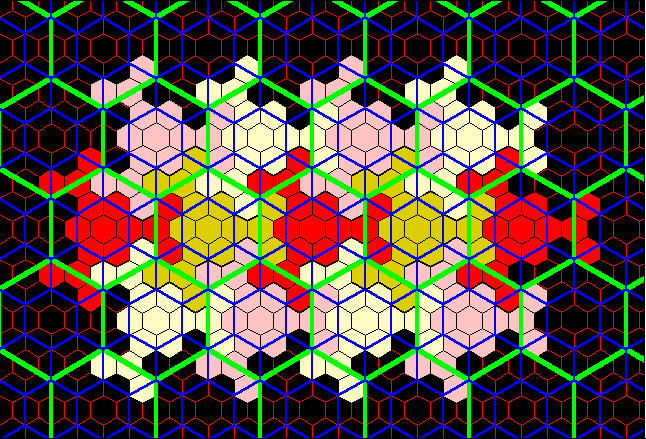Figure 6b.  Principle of 4.  Fractal generation procedure suggested by tiling pattern.  Fractal dimension when iteration is carried out infinitley is:  1.5849625

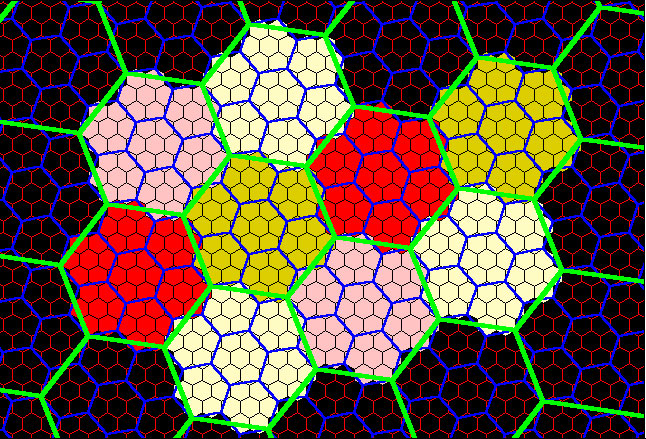Figure 6c.  Principle of 7.  Fractal generation procedure suggested by tiling pattern.  Fractal dimension when iteration is carried out infinitley is:  1.1291501


One might imagine each of these as a "hextree" on which to hang spatial information in association with the material about the Earth already present in Google Earth.  Figure 7a shows the pattern of Figure 6a applied to the Google Globe.    Figure 7b shows that pattern in association with the underlying terrain.  If the tiles could be made to all be the same size, and not scaled to the lat/long graticule, then distant tiles brought into focus would enlarge--that feature is often a desirable factor when thinking of navigating in real Earth based space.  What looks small on the horizon becomes larger as it is approached!

Figure 7a.  One scheme for creating close-packed regions.  Fractal dimension:  1.2618595

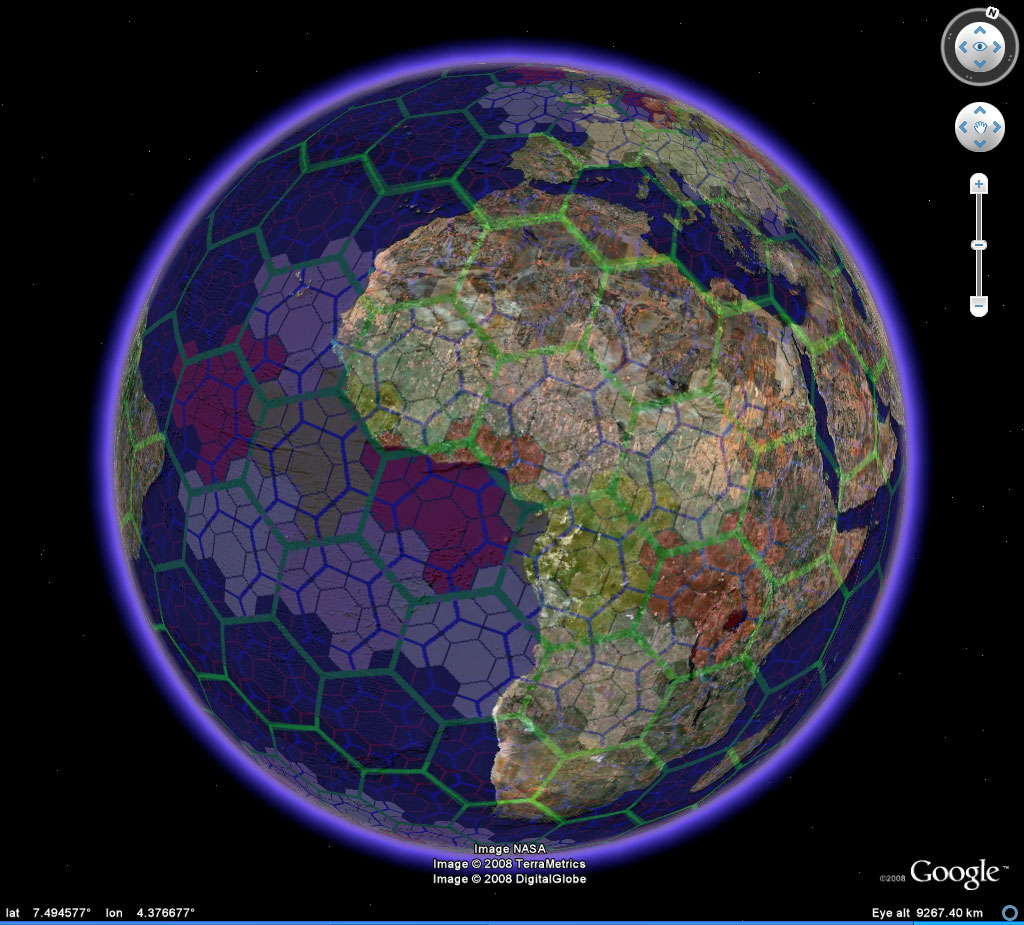Figure 7b.  Regions in association with topography and other terrestrial and oceanic information.  Transparency can be important in turning theory into practice.


Questions for further thought:
  • Different methods for creating regions exist in different disciplines.  These should be explored and mapped on the Google Globe.
  • When the U.S. Census used GBF DIME files in the 1980 census they apparently did not take account of the Jordan Curve Theorem causing geocoding errors.  The Google Globe offers great opportunity to get major theorems of topology, geometry, and algebra in front of a diverse audience of potential users who might make extraordinary use of these theorems.
  • Contour integration might be realized by cutting holes in polygons.
  • Coordinate system changes could be important in a variety of ways.
The Google Globe, as well as Google Earth, has great promise for the visualization of complex mathematical ideas.   Again, visualization on the entire sphere, which requires transparency, is important in diverse fields of endeavor.


REFERENCES: 
Arlinghaus, Sandra L. and Arlinghaus, William C.  Spatial Synthesis, Volume I, Book 1.  Centrality and Hierarchy.  Ann Arbor:  Institute of Mathematical Geography.  2005.

Arlinghaus, Sandra L.  "Fractals take a central place," Geografiska Annaler, 67B, (1985), pp. 83-88. Journal of the Stockholm School of Economics.  1985.

Arlinghaus, Sandra L.  "Micro-cell Hex-nets"   Solstice:  An Electronic Journal of Geography and Mathematics, Institute of Mathematical Geography  Previous link is to original TeX code sent around via e-mail; click on the next link to see scanned images of typeset printout made from the TeX file:  Micro-cell Hex-nets  1993.

Arlinghaus, Sandra L. and Arlinghaus, William C.  "The fractal theory of central place hierarchies: a Diophantine analysis of fractal generators for arbitrary Löschian numbers," Geographical Analysis: an International Journal of Theoretical Geography. Ohio State University Press. Vol. 21, No. 2; pp. 103-121.  1989.

Arlinghaus, Sandra L. and Arlinghaus, William C.   "Spatial Synthesis Sampler. Geometric Visualization of Hexagonal Hierarchies:  Animation and Virtual Reality."  Solstice:  An Electronic Journal of Geography and Mathematics, Institute of Mathematical Geography, Ann Arbor, MI.  Semi-finalist, Pirelli INTERNETional Award Competition.  2004.

Christaller, Walter.  Die zentralen Orte in Süddeutschland:  Eine ökonomisch-geographische Untersuchung über die Gesetzmässigkeit der Verbreitung und Entwicklung der Siedlungen mit städischen Funktionen.  Jena:  Gustav Fischer Verlag.  Doktor-Dissertation.  1933.

Dacey, Michael F.  The geometry of central place theory. Geografiska Annaler, B, 47, 111-124.  1965.

Lösch, August.  The Economics of Location.  Yale University Press, 1954.

Marks, Mano (Google), October 23, 2008:  Quadtree reference from "advanced" workshop.

Marshall, John U.  The Löschian Numbers as a Problem in Number Theory. Geographical Analysis 7, 421-426.  1975.

Nystuen, John D.  Personal communication, the importance of tiles on the horizon coming into view to show more.  2008 and earlier.

Weiss-Malik, Michael (Google), October 23, 2008:  stated that the underlying projection has singularities at the poles.

Dr. Arlinghaus is Adjunct Professor at The University of Michigan, Director of IMaGe, and Executive Member, Community Systems Foundation.

Solstice:  An Electronic Journal of Geography and Mathematics, Institute of Mathematical Geography, Ann Arbor, Michigan.
Volume XIX, Number 2.
http://www.InstituteOfMathematicalGeography.org/
Persistent URL:  http://deepblue.lib.umich.edu/handle/2027.42/58219