| SOLSTICE: An Electronic Journal of Geography and Mathematics. (Major articles are refereed; full electronic archives available). Persistent URL: http://deepblue.lib.umich.edu/handle/2027.42/58219 |
 |
The Platonic Solids:
Earth-sculpture Anchored at Easter Island (Barr's Condition)
Sandra Lach Arlinghaus
Adjunct Professor of Mathematical Geography and Population-Environment Dynamics
School of Natural Resources and Environment
The University of Michigan
| Download
the linked kmz file
and load it into
Google Earth to drive around the model as you read this
article. Mathematical Geography and Global Art: The Mathematics of David Barr's 'Four Corners Project. |
David Barr has built a global structure based on the geometry of the ancients. His "Four Corners Project" embeds a partially virtual tetrahedron in the Earth. The vertices of the sculpture are real. In a fascinating odyssey, Barr and his team travelled to the Four Corners of the Earth over the ten-year period it took to complete the sculpture. The process involved a host of people from far-flung academic and geographic backgrounds. The tale is told in his recent book called Crossing Lines. The story of the mathematics behind the determination of these corners is set forth in IMaGe Monograph #1 (Arlinghaus and Nystuen). The latter part of that monograph involves calculations and logical arguments that were difficult to imagine and to draw at the time that book was written (1985). Current software permits easy visualization of that material and also offers different ways to analyze the situation. It is to this task that the current article is devoted.
For a variety of historical and cultural reasons, Barr chose to place one of his four corners on Easter Island in the Pacific Ocean. Nystuen calculated locations for the remaining three vertices, given the initial constraints that:
- One vertex must be on Easter Island
- All
vertices must be on land
| Easter Island (Pacific Ocean): | -27.10556º latitude, -109.425º longitude |
| Kalahari Desert (Africa): | -27.51º
latitude, 24.1º
longitude |
| Greenland
ice cap: |
72.64º
latitude, -41.92º
longitude |
| Irian
Jaya (New Guinea): |
-2.11º
latitude, 137.39º
longitude |
Small marble tetrahedra, representing the "corners" of a giant tetrahedron were planted by Barr and company at, or near, each of these locations. The ceremony surrounding these events, and a full chronicle of them, appears elsewhere ( Barr, 2008; Arlinghaus and Nystuen, 1986 and 2009; Archives of American Art, Smithsonian Institution, 1985). In this article, visualization of some of the material originally in the 1986 work cited above is substantially improved and in fact serves as the basis for a different form of "proof" that Barr's choice of the tetrahedron was the only one of the Platonic solids that could meet his two initial conditions.
TERRAE ANTIPODUM
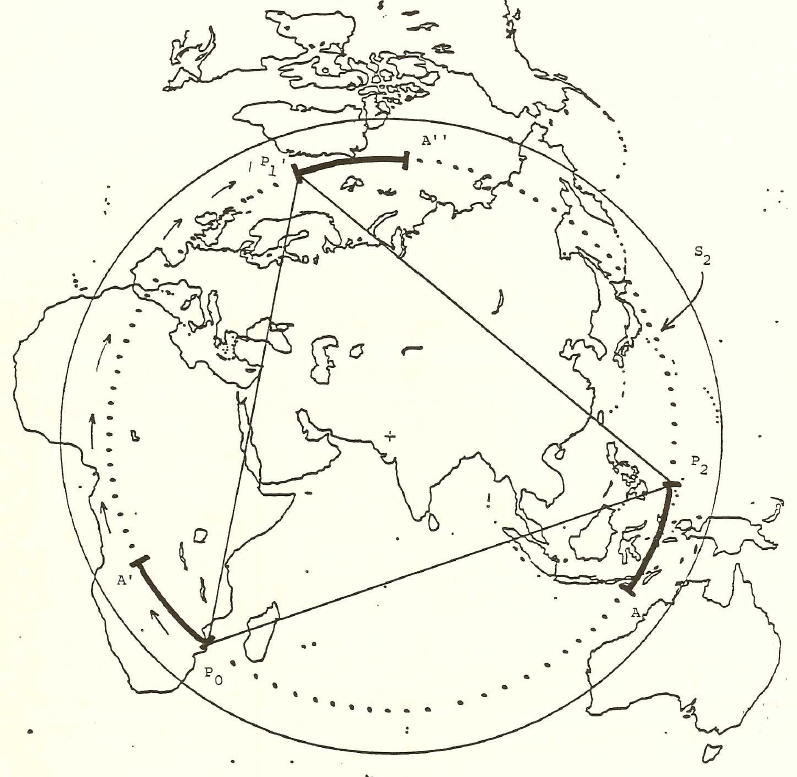
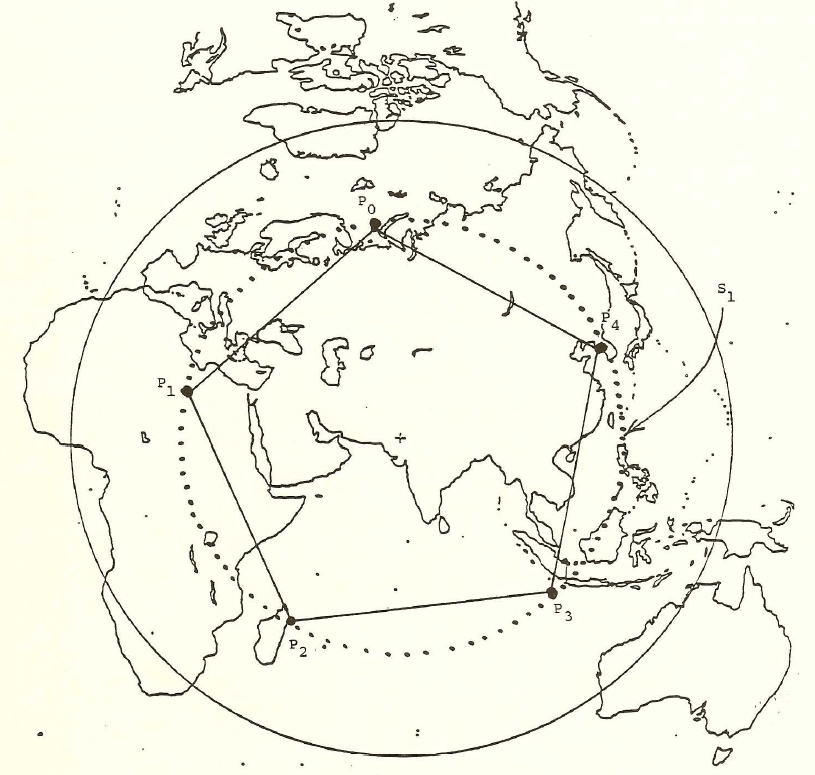
Nystuen made his original calculations with the aid of the antipodal point of Easter Island in order to force all calculations into the same hemisphere. Earlier, Tobler [1961] had made a world map on a Möbius strip and noted that a pin poked on the strip identified pairs of antipodal points on the globe. This strategy showed a map of half the world. The author made a full world map [1985], on a flat sheet of paper, using the Möbius transformation (Figure 1a). That map appears in Monograph #1. It was used in making arguments about the uniqueness of Barr's choice of a tetrahedron within the set of Platonic solids: tetrahedron, cube, octahedron, dodecahedron, and icosahedron. Figure 1b below shows the process realized on the Google Earth Globe. With the kmz file open, change the amount of transparency in the overlay to see different patterns of antipodality on the globe. The animation in Figure 1 suggests a few of these patterns--notice for example the antipodal land pairs in Argentina and China. Again, this map is used in the visual arguments below to illustrate difficulties posed had any Platonic solid other than the tetrahedron been chosen by Barr under the constraints that one vertex be situated at Easter Island and that all vertices be situated on land.
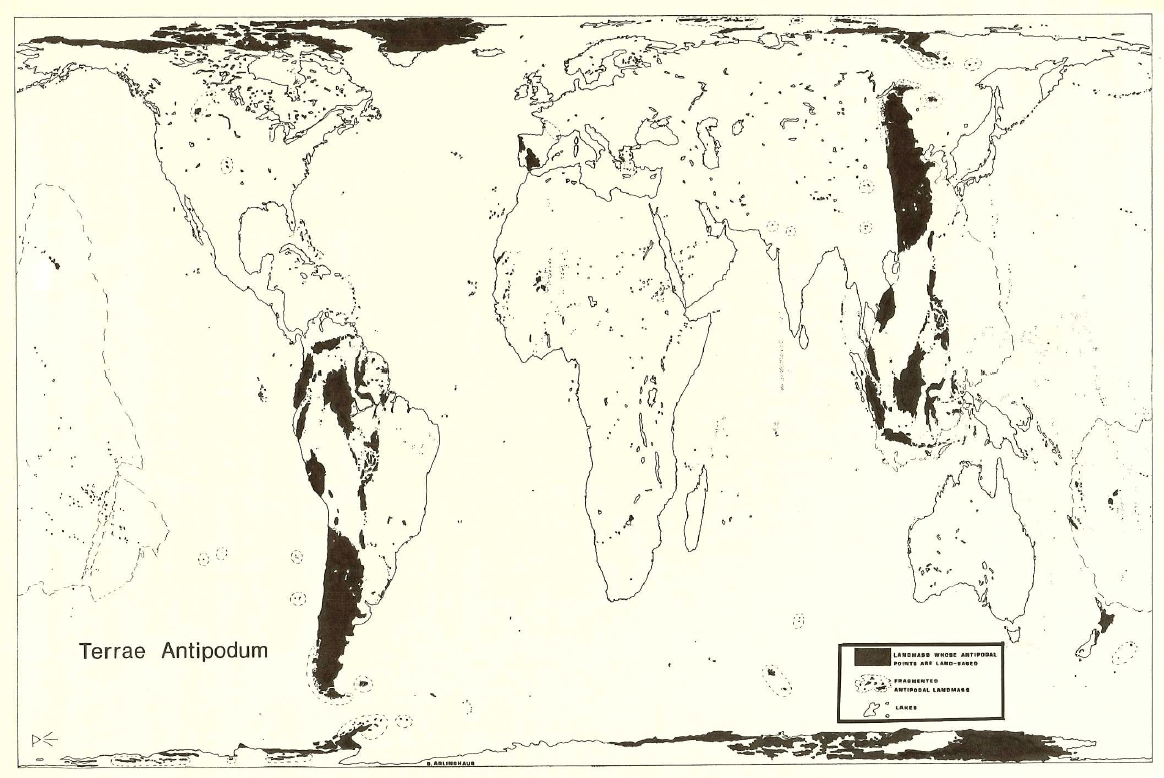 Figure 1a. Map of antipodal lands from Monograph #1, 1986. |
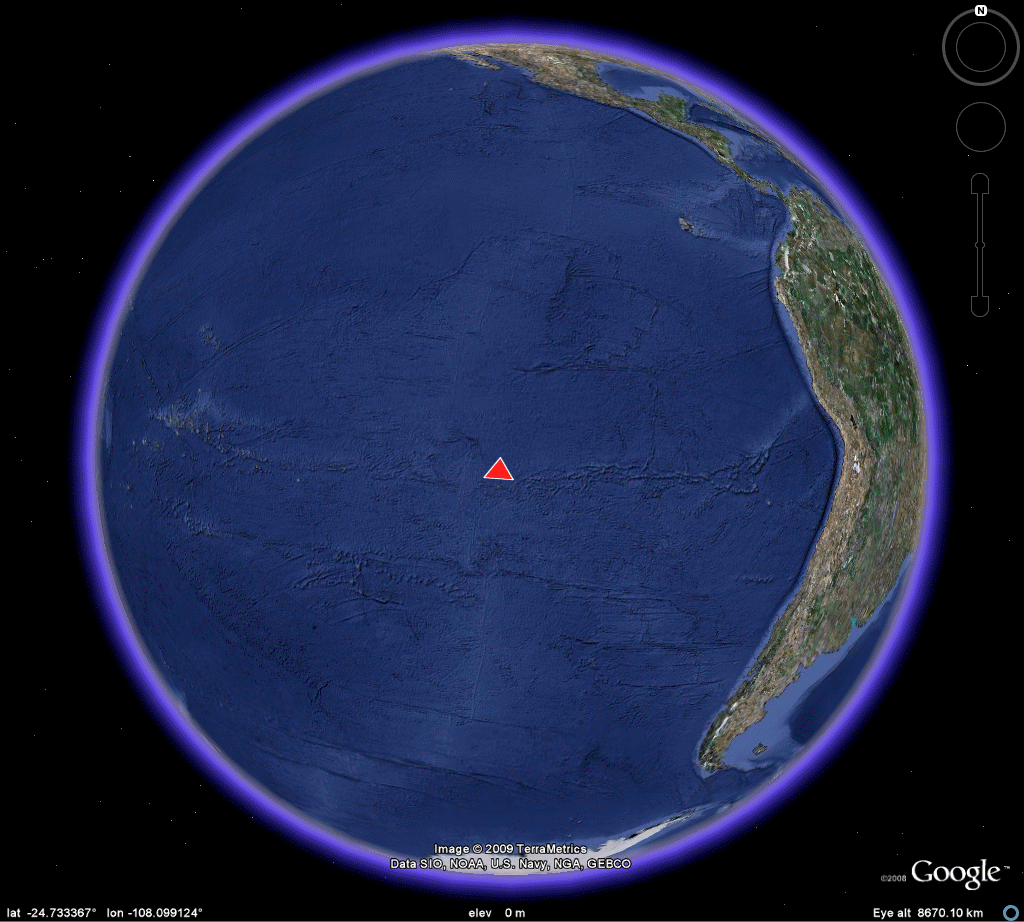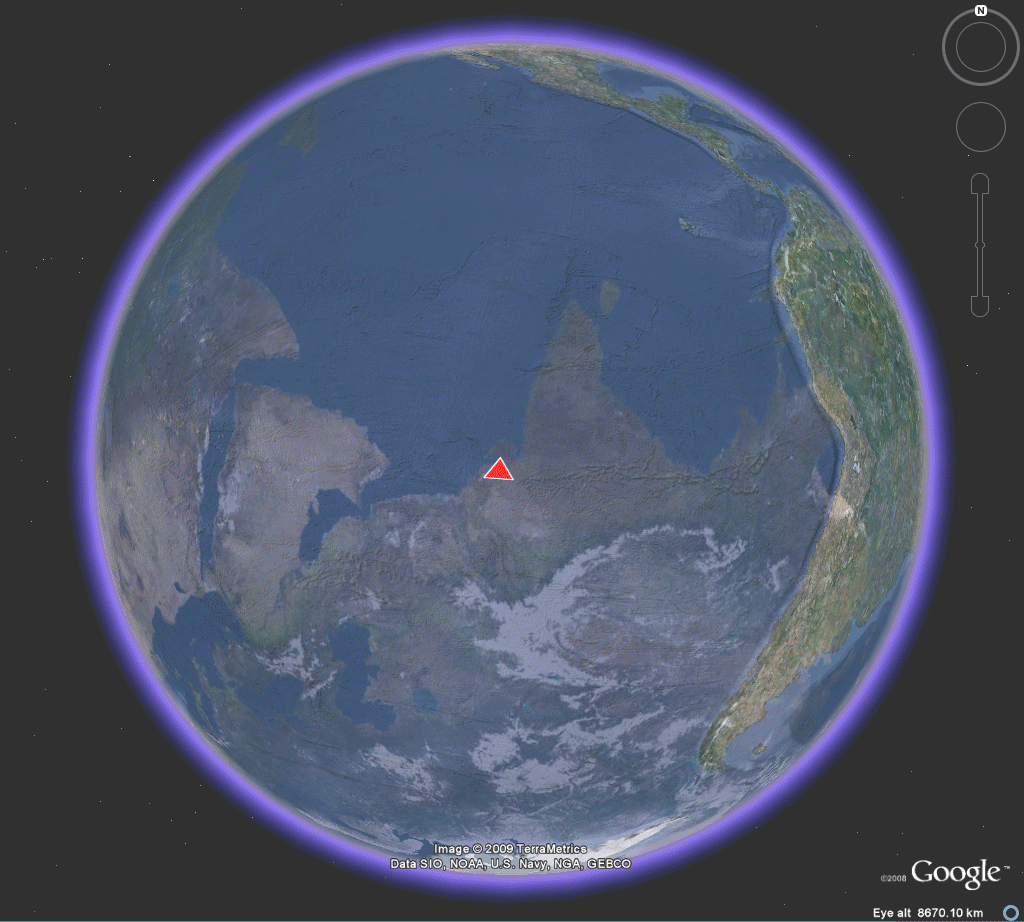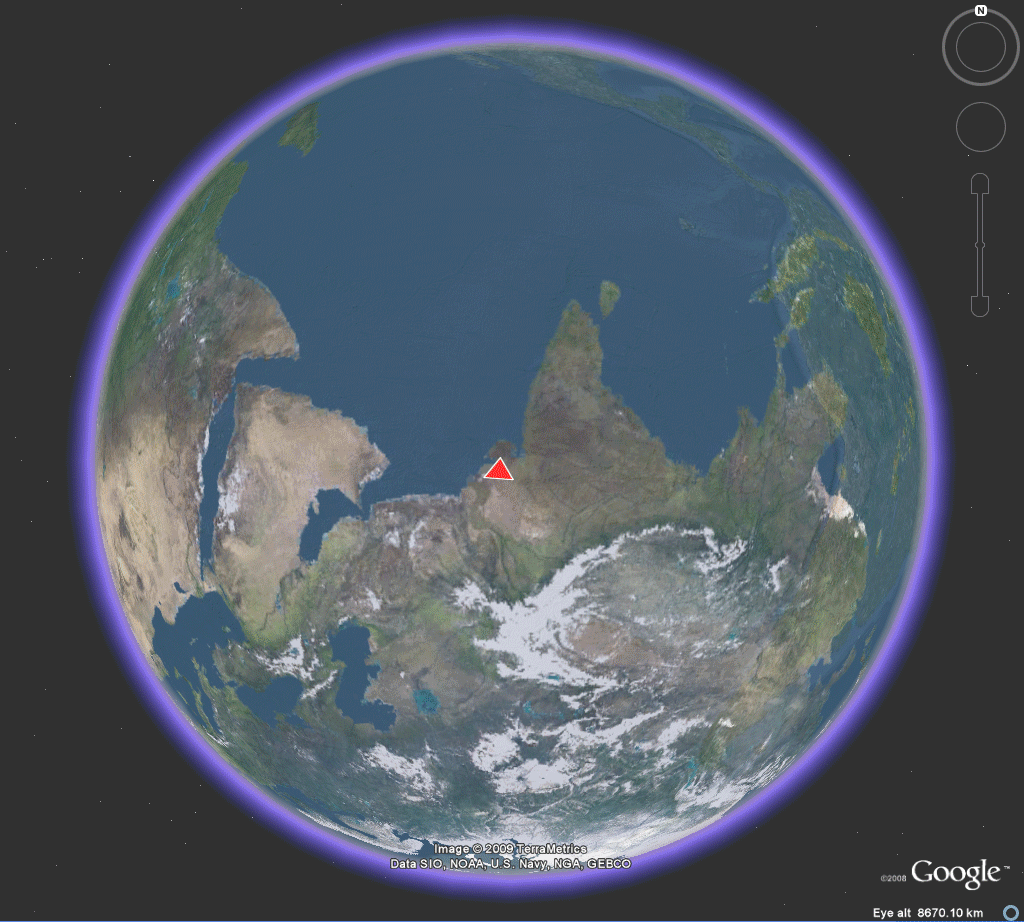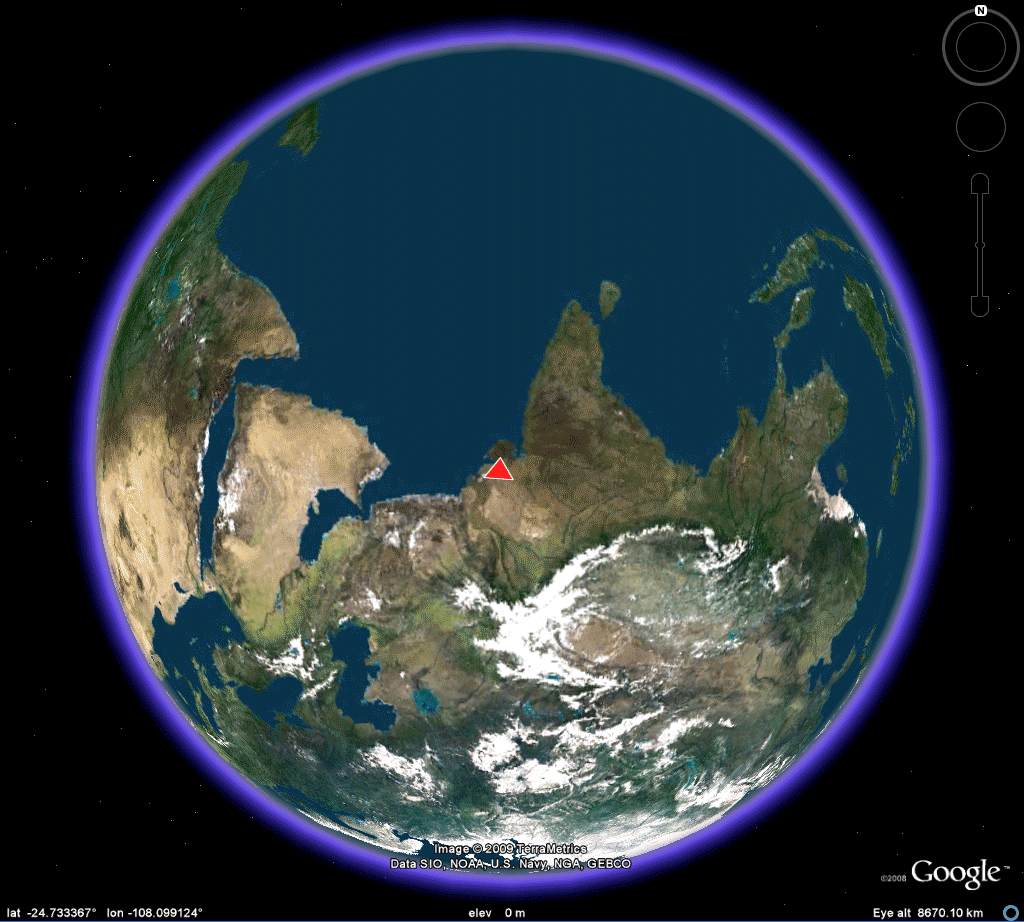 |
TETRAHEDRON
Figure 2 shows Nystuen's tetrahedral locations mounted on the Google Earth Globe. When the linked kmz file, in the table at the top, is loaded into Google Earth, the reader can drive around the model and zoom in on the various locations to take a look at the surrounding terrain. Be aware, however, that these original calculations were made awhile ago and may have been rounded off to facilitate calculations (thus placing a vertex slightly offshore and so forth). Also, please note that the quality of surveying equipment employed may have set the piece off the calculated site. The final caveat is simply that once on site, Barr and crew may have decided to shift the location of the corner for aesthetic or other reasons. All of these minor issues do not affect the sculpture at the global or broad regional view. They may, however, affect a close-up view, either in Google Earth or in the field.
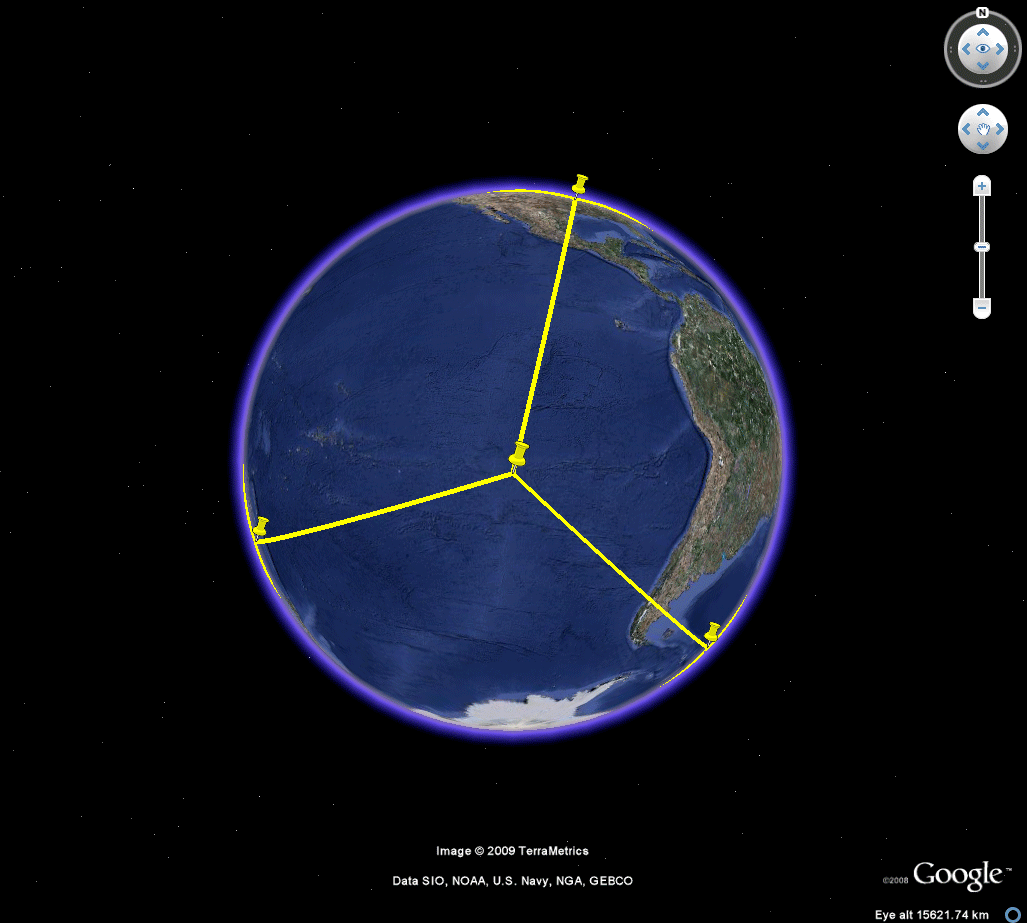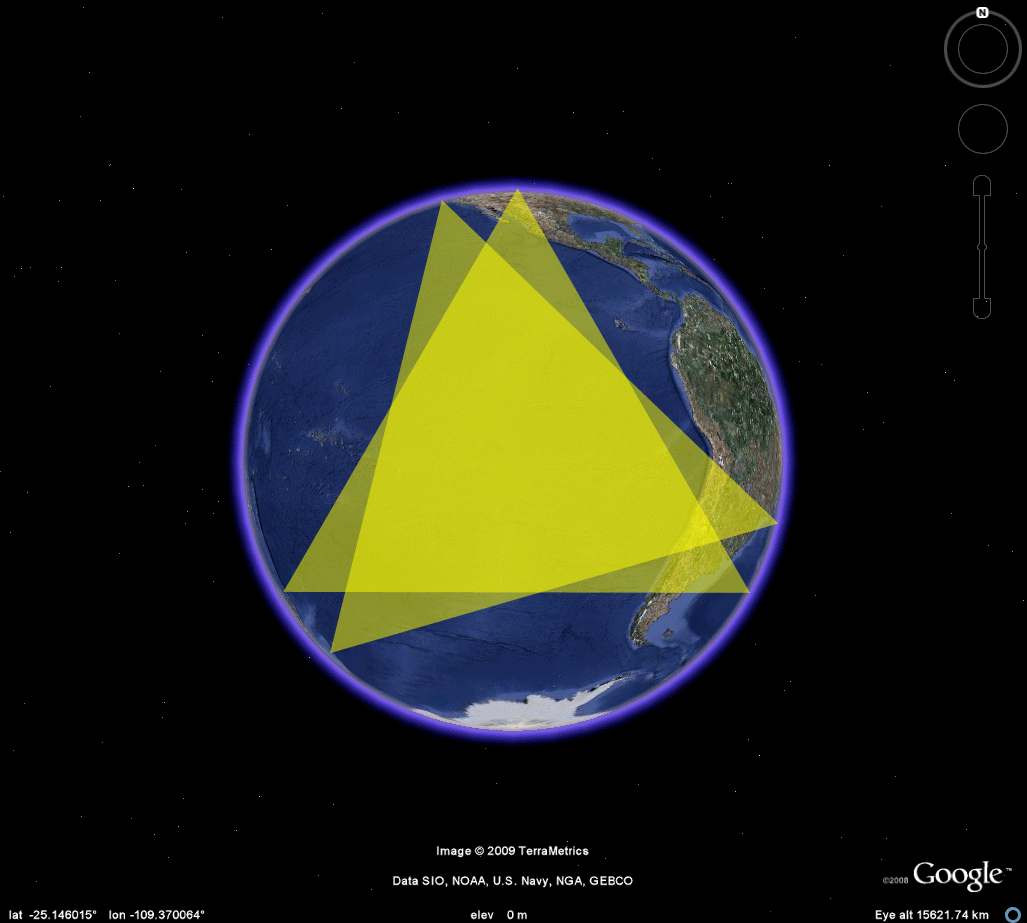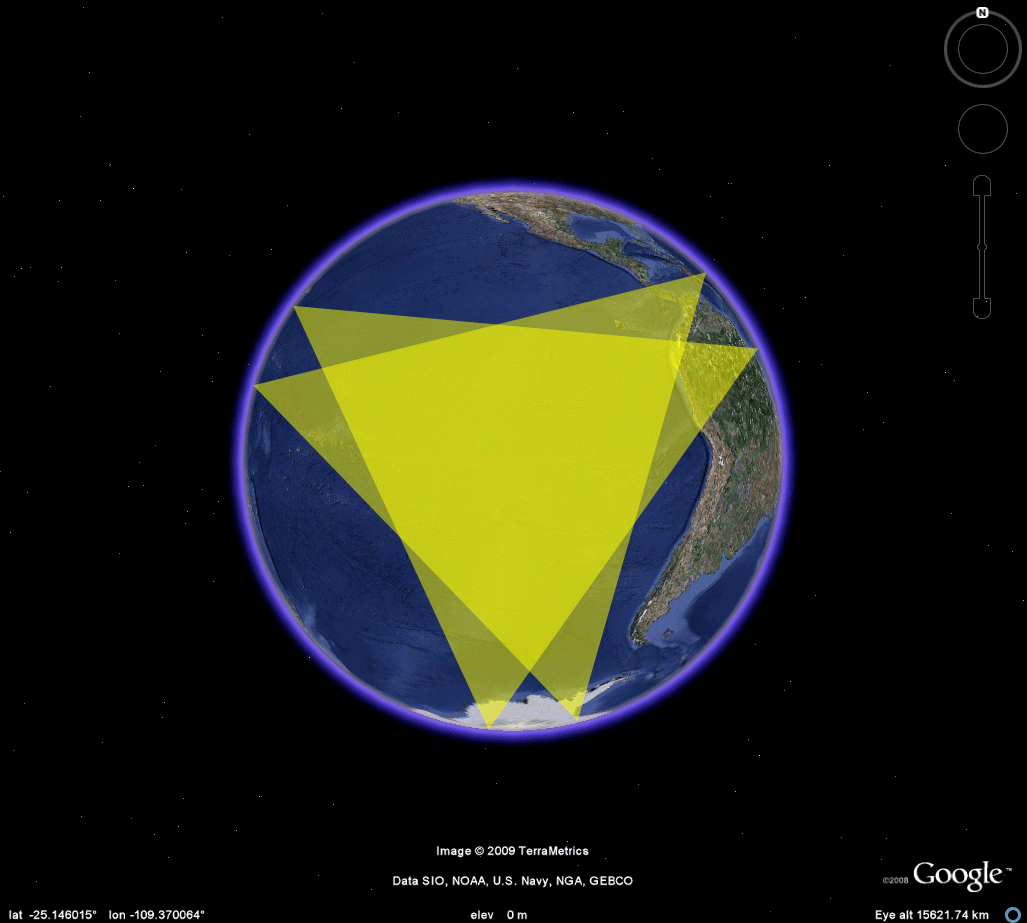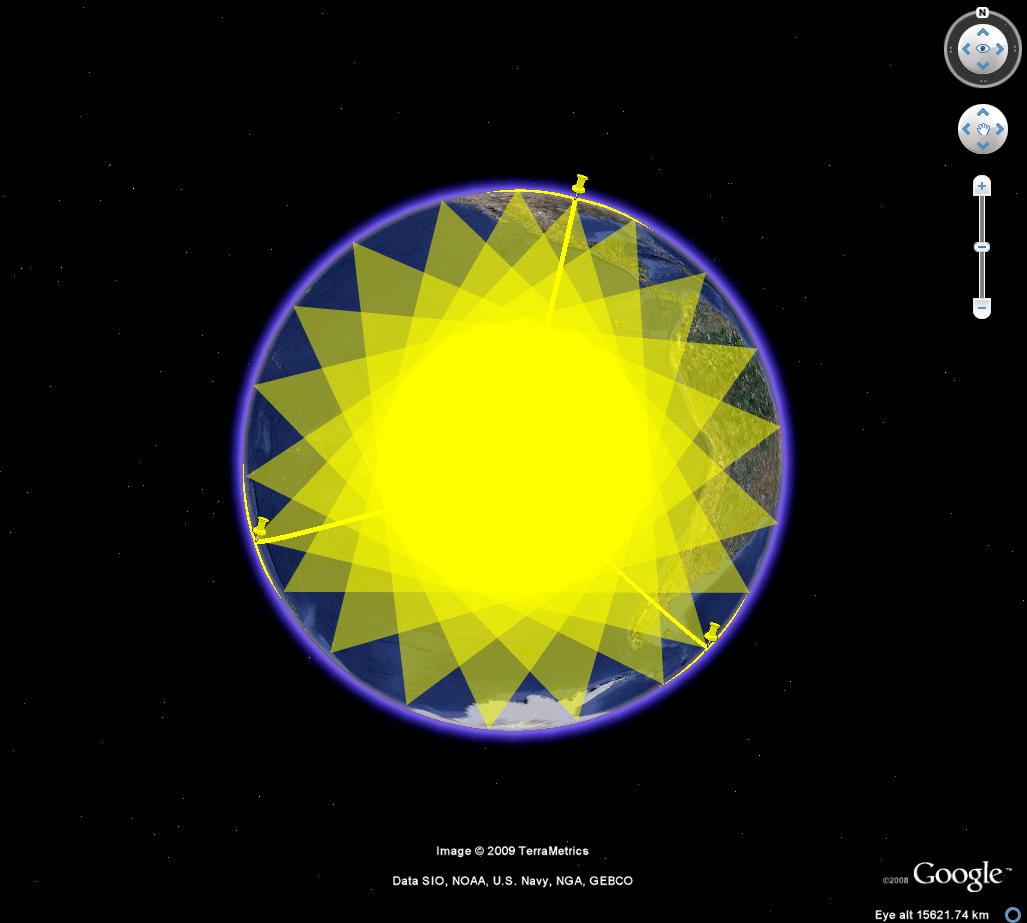
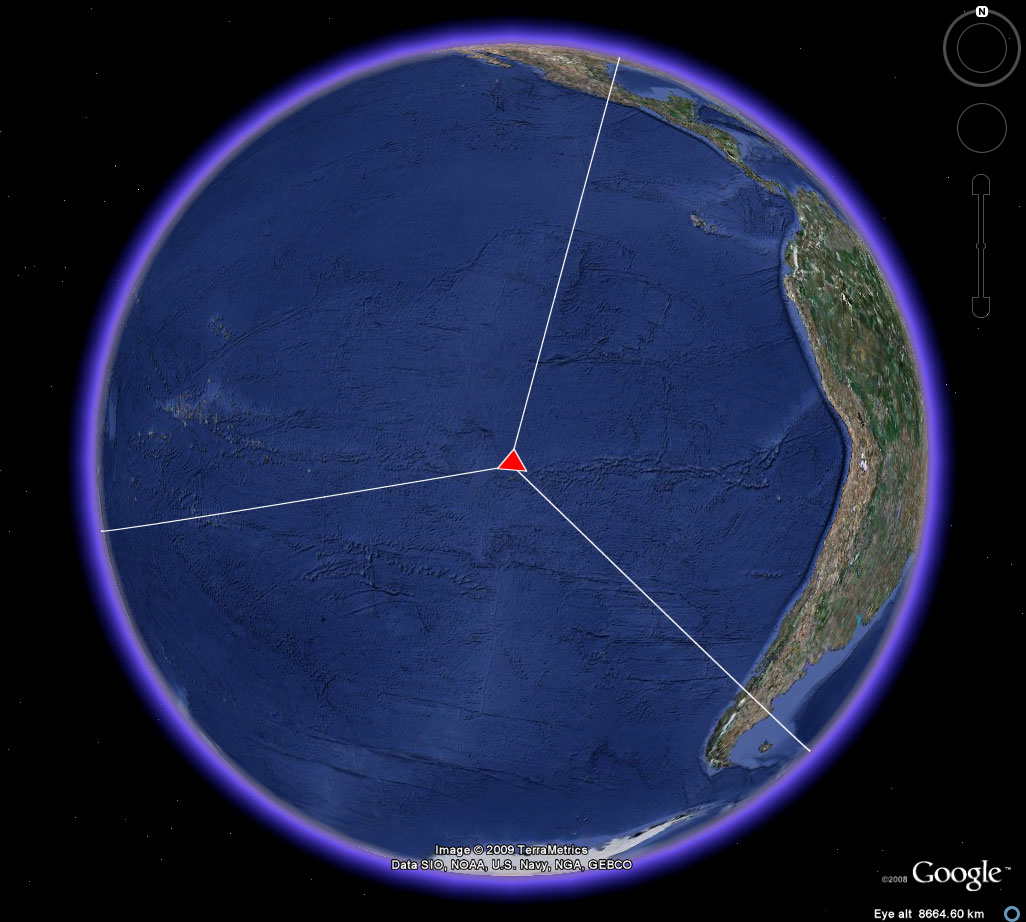 Figure 2a. A view of four corners for the location of a tetrahedron in the Earth-sphere. Easter Island. |
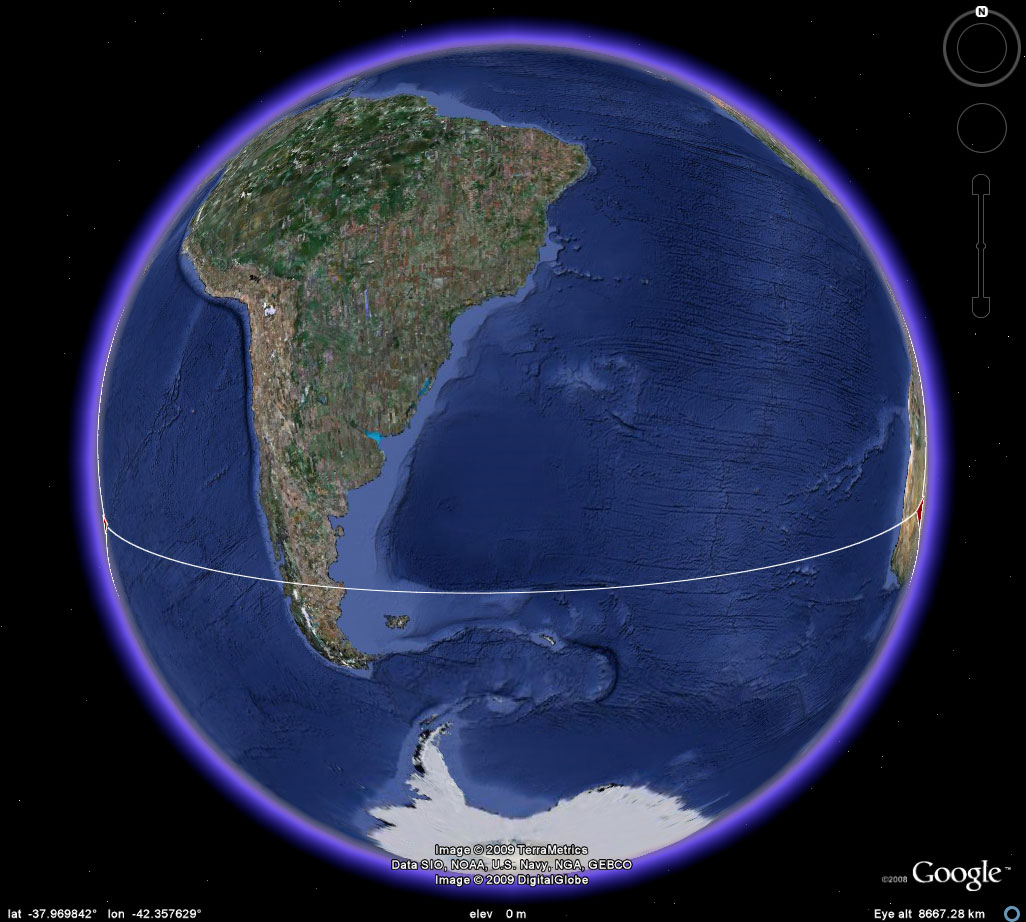 Figure 2b. A view of four corners for the location of a tetrahedron in the Earth-sphere. Easter Island to the Kalahari Desert. At most two corners can be viewed simultaneously in Google Earth when the skin of the Earth is visible. |
 Figure 2c. A view of four corners for the location of a tetrahedron in the Earth-sphere. Easter Island to the Kalahari Desert. At most two corners can be viewed simultaneously in Google Earth when the skin of the Earth is visible; here, the skin from Figure 2b has been removed with all else the same. Notice that now all four corners are visible. |
 Figure 2d. A view of four corners for the location of a tetrahedron in the Earth-sphere. Rotate the globe to better view the corners simultaneously. |
 Figure 2e. A view of four corners for the location of a tetrahedron in the Earth-sphere. Add edges to get a better view of the embedding of the sculpture in the globe. John Nystuen asked also to have some sort of continental context, for orientation, added to the image. Figure 2f illustrates one approach to that. |
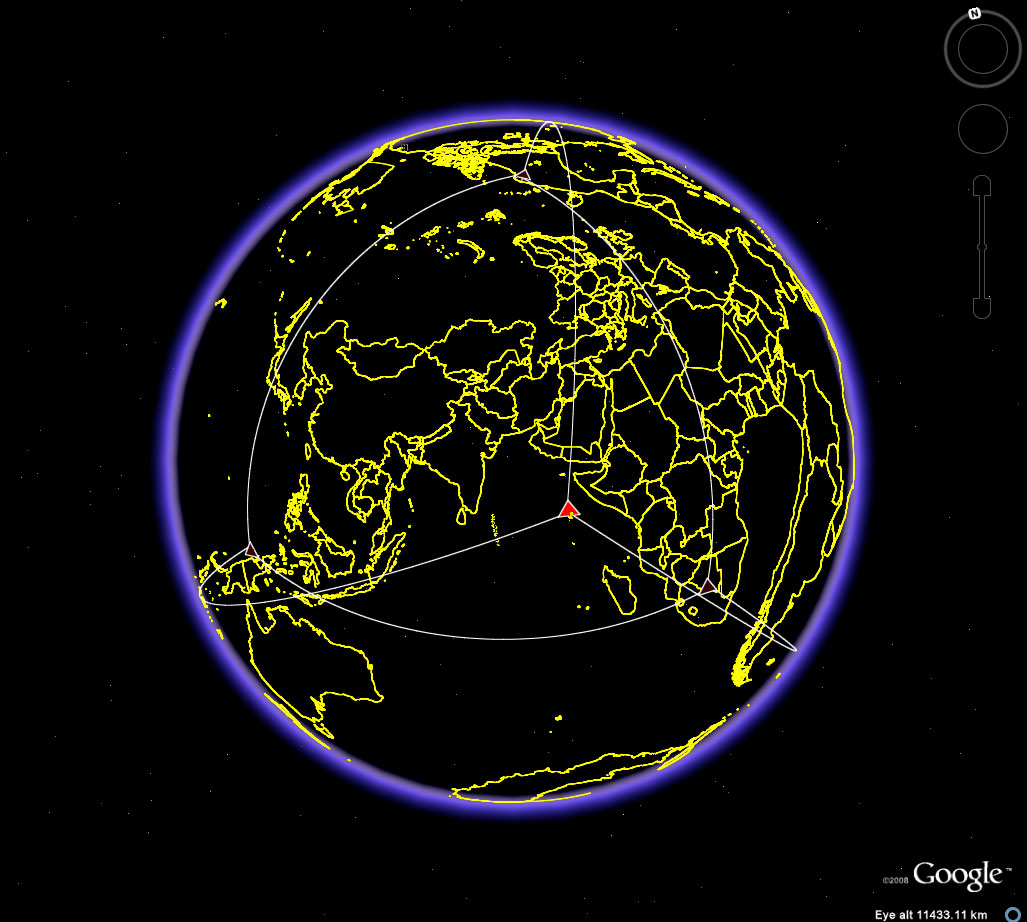 Figure 2f. A view of four corners for the location of a tetrahedron in the Earth-sphere. Add edges to get a better view of the embedding of the sculpture in the globe and reference them to continental outlines, imported as a shapefile, so that they, too, show through the Earth-sphere. Easter Island is the bright red vertex closest to the center; the vertex to the left and on the other side of the globe is on Irian Jaya. The vertex in the Kalahari Desert is on the back side of the globe (east/west pattern in Africa is thus inverted). |
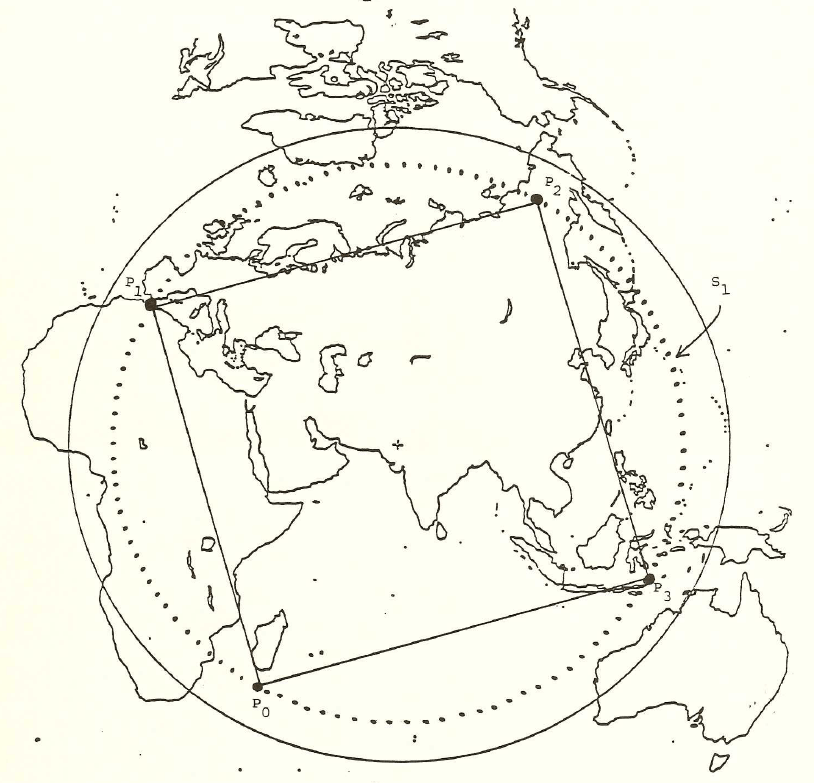
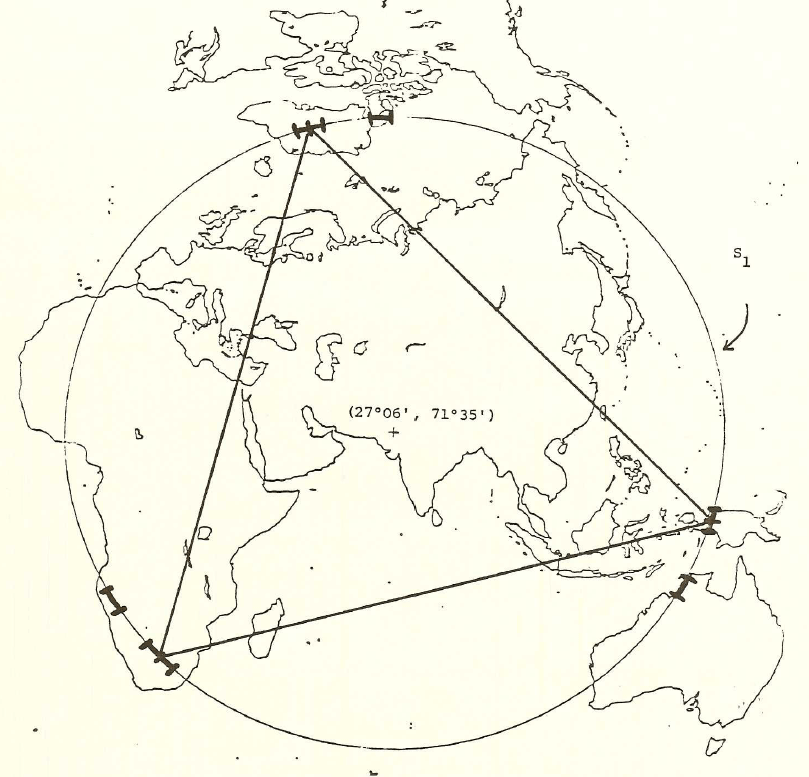 Figure
2.g. An
equilateral triangle cut from a piece of paper was
used as an aid in
locating the collection of points which could
serve as vertices of the
proposed sculpture. By placing its corners
on the circle drawn on
the azimuthal map, one can rotate the triangle and
discover the
collection of points which satisfy the condition
that they all fall on
dry land. This procedure confirmed that
Barr's own discovery of
the location set {Easter Island, Kalahari Desert,
Greenland Ice Cap,
and New Guinea} was feasible. Again, only
half the sphere is
visible so that one must imagine the Easter Island
location in this map
centered on its antipodal point in the Thar
Desert.
|
THE REMAINING PLATONIC SOLIDS
The locations of the vertices for the remaining Platonic solids were calculated using Google EarthGrid, an online calculator. Figure 3a shows the screen from this useful tool. Simply fill in the coordinates above for Easter Island as the "anchor" for the sculpture, and any one of the other pairs of coordinates as the "header." (Google Earth sees only six decimal places; entering more does apparently not increase locational precision.) Then, download the file that is returned and load it into Google Earth. Remove extraneous edges. The .kmz file linked at the top of this page contains these calculated images for each of the Platonic solids.
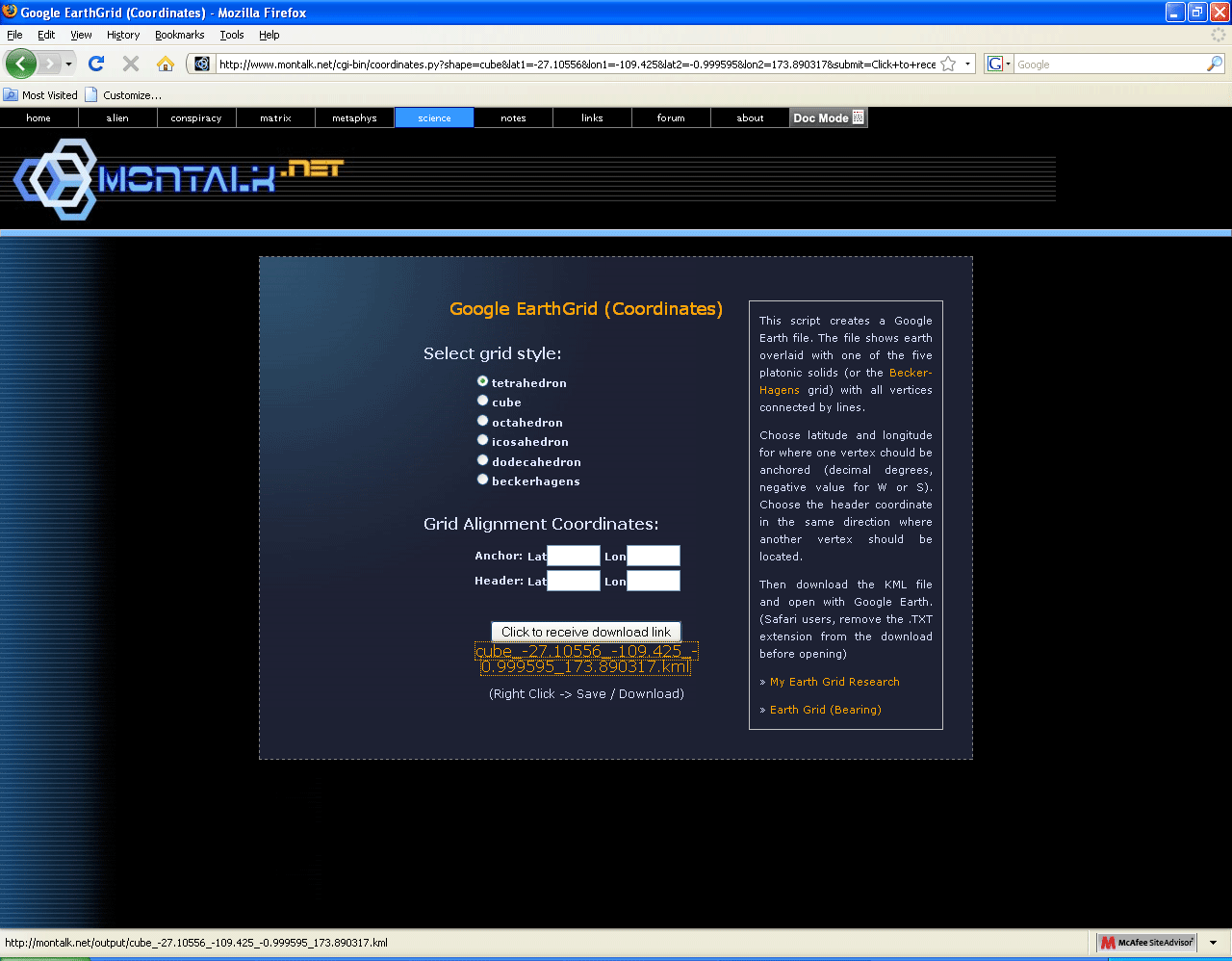 Figure 3a. Screen capture from Google EarthGrid. See link in Reference section. |
Figures 3b, 3c, 3d, and 3e show the results of using the calculator with Easter Island coordinates as the anchor and the Greenland coordinate as the header for each of the cube, octahedron, dodecahedron, and icosahedron. In the original 1986 document, there are no images of this sort. There are rough drawings of polyhedra but no drawings of polyhedra embedded in a globe.
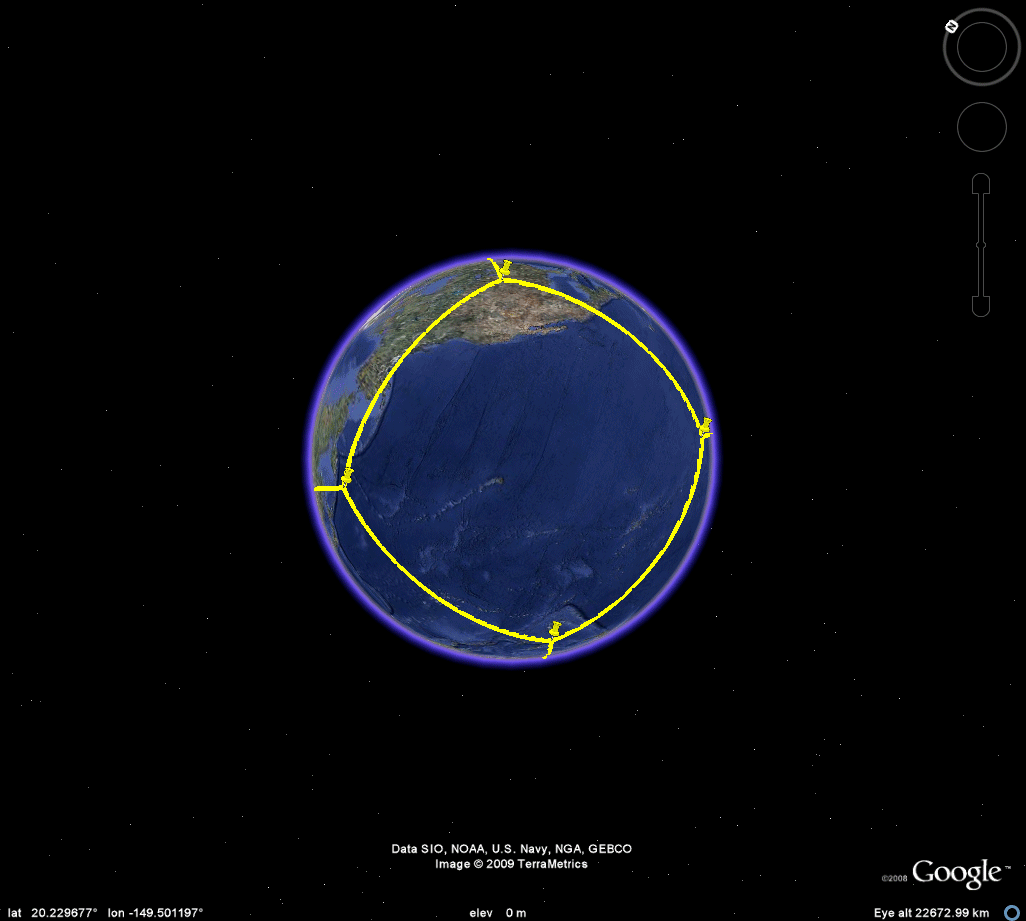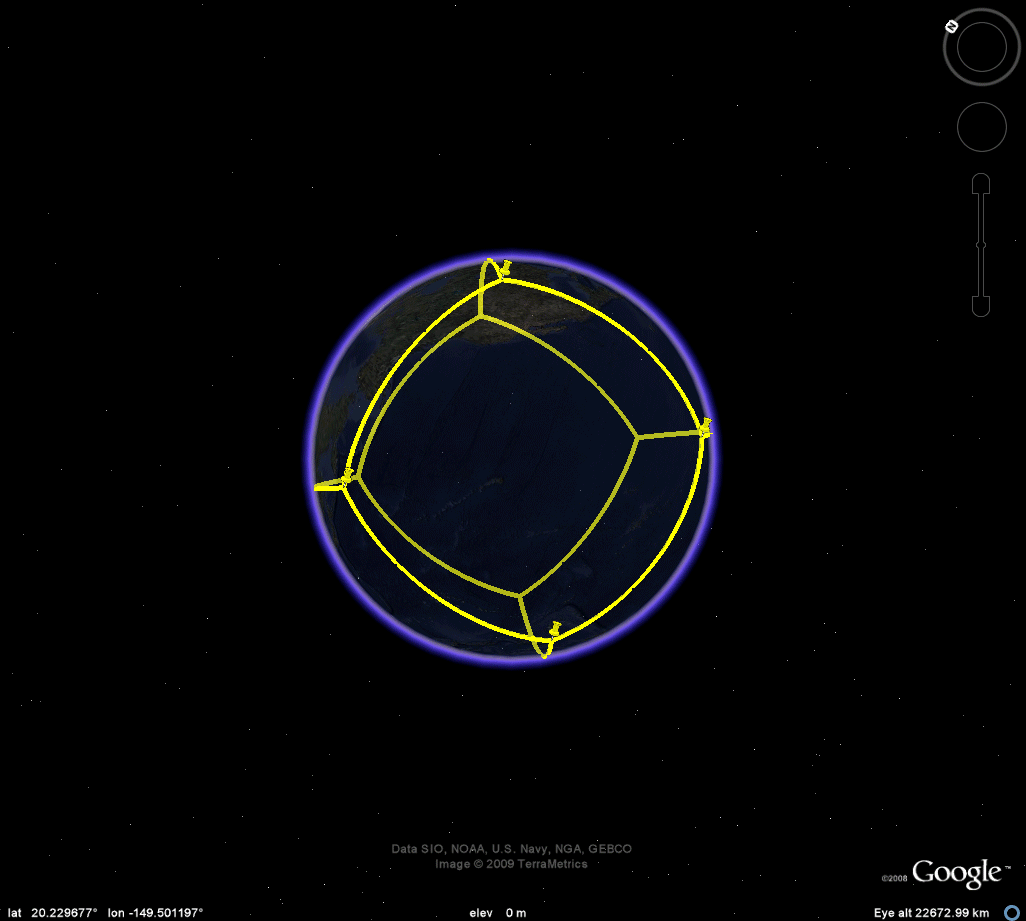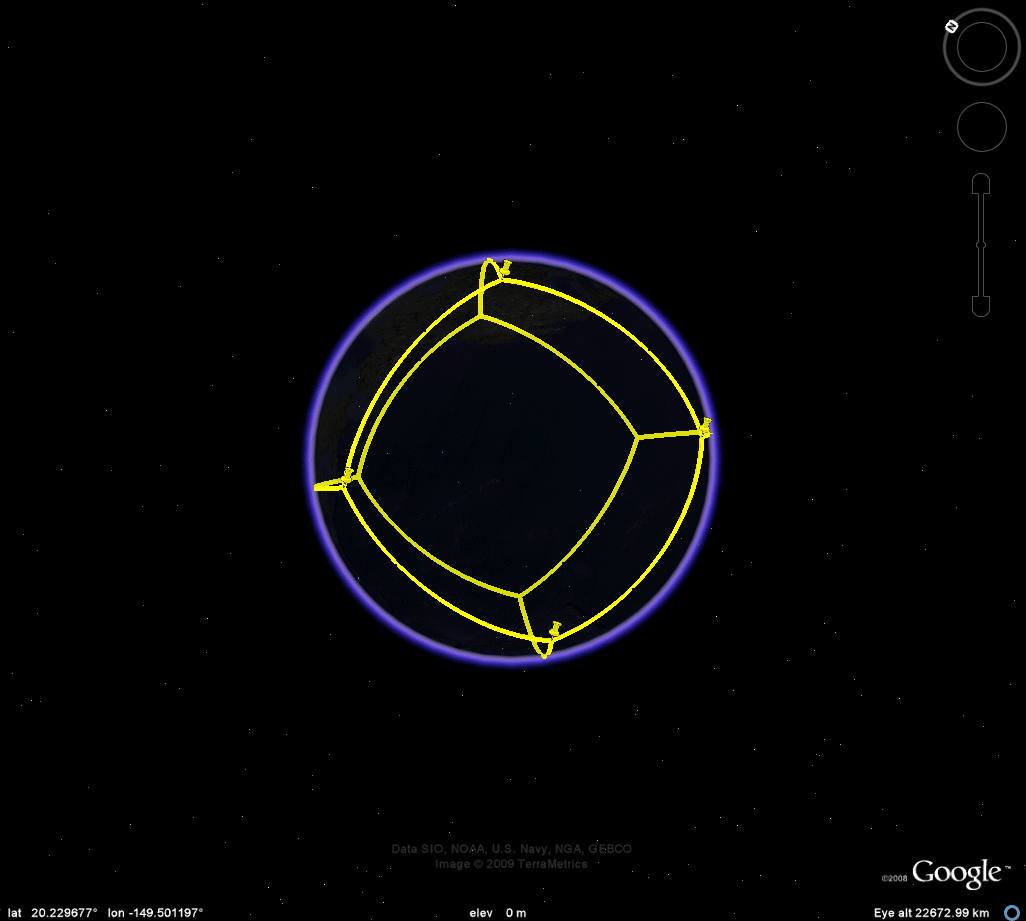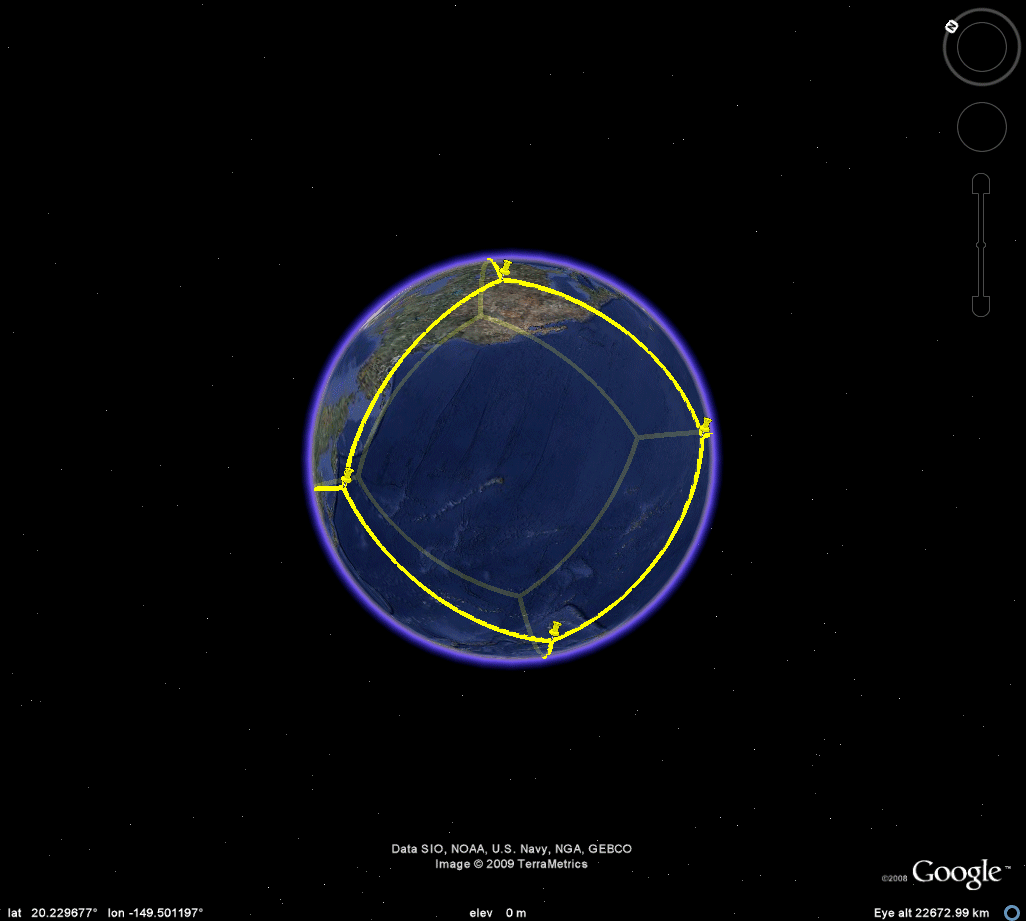 Figure 3b. Cube. |
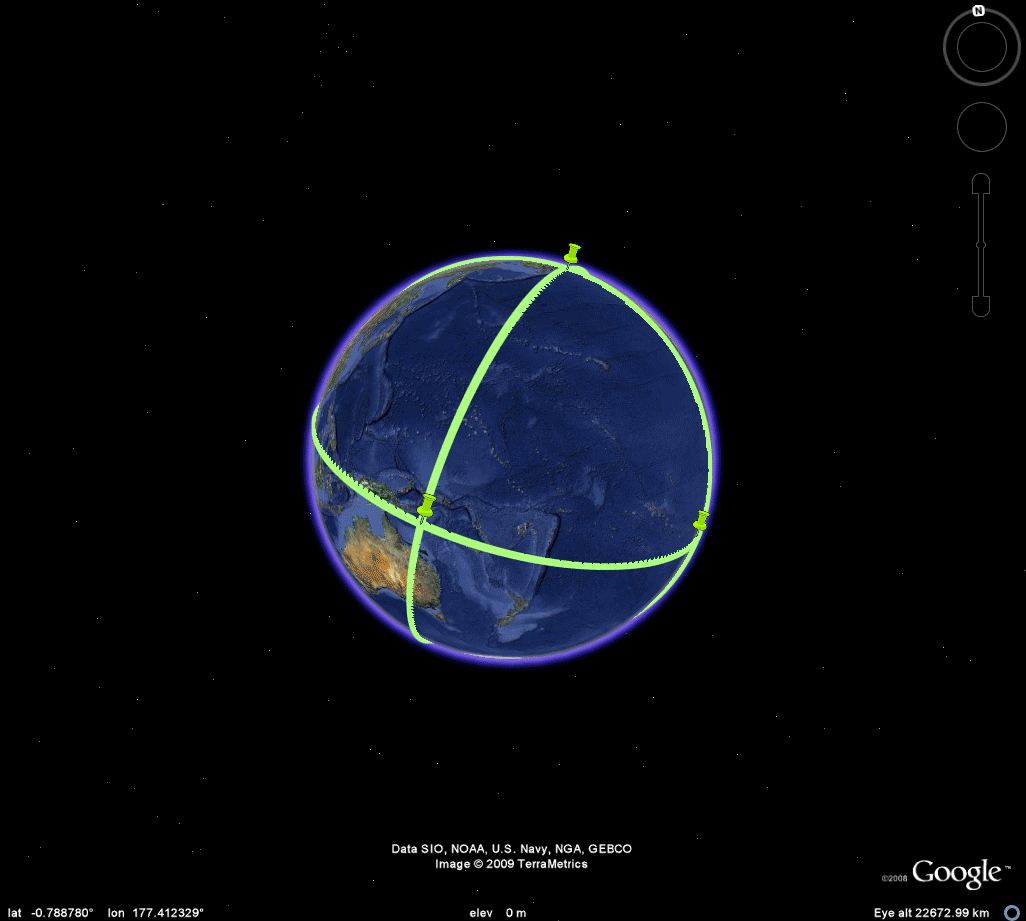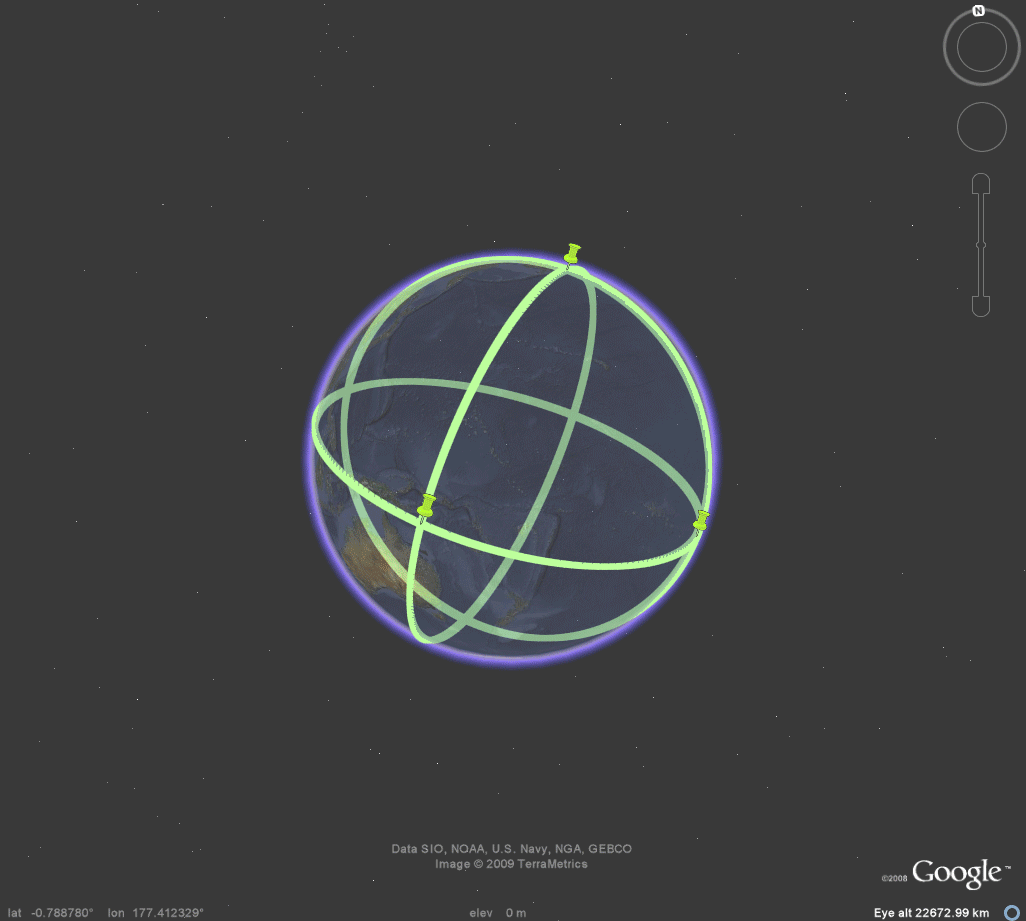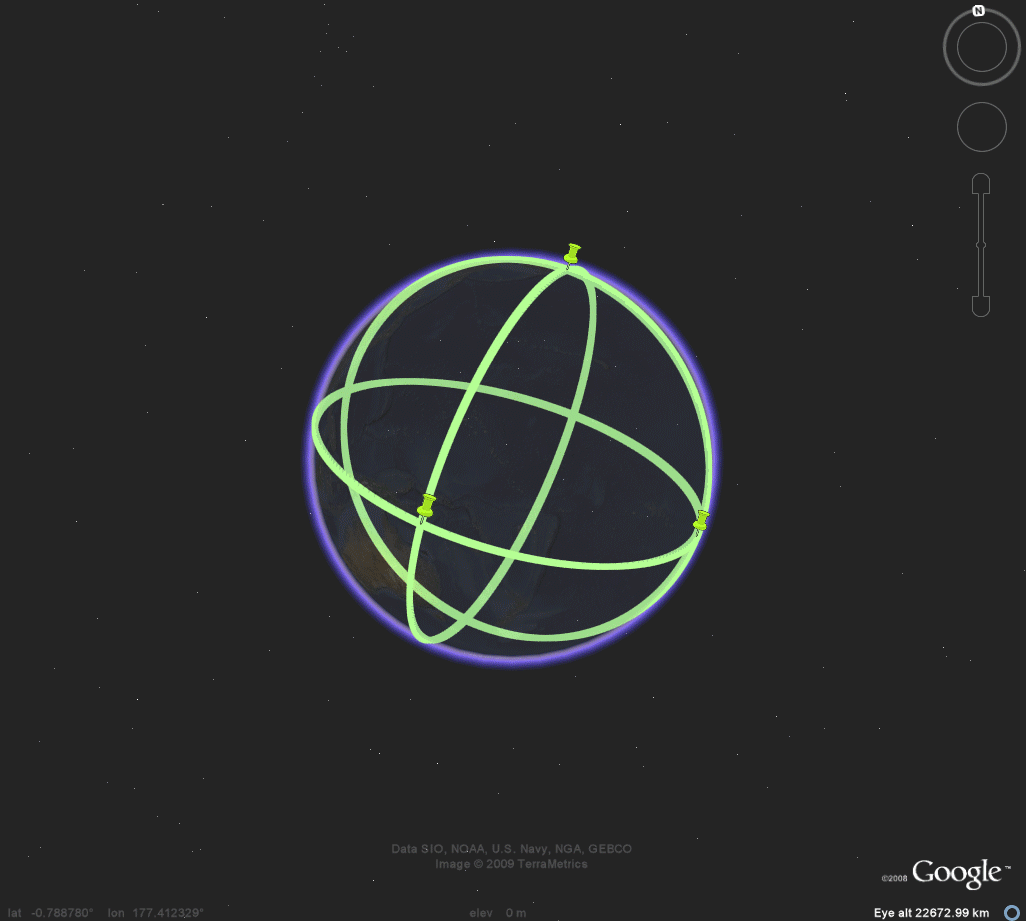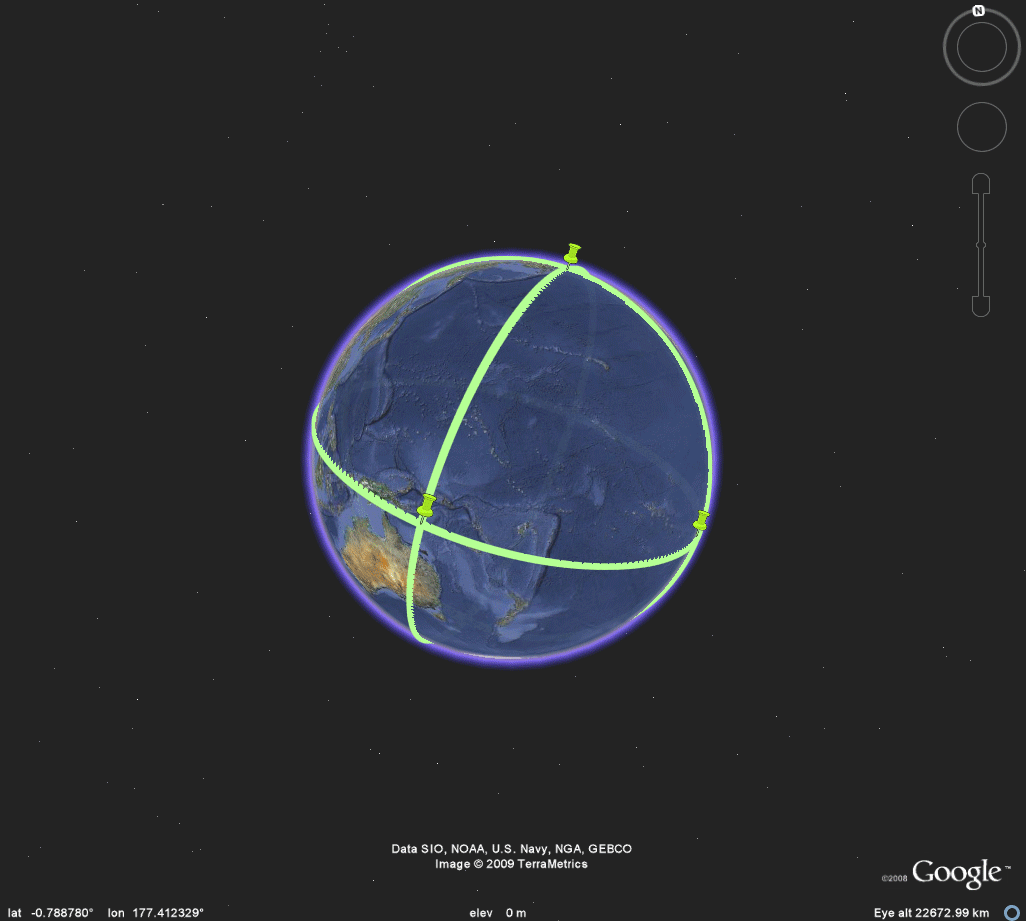 Figure 3c. Octahedron. |
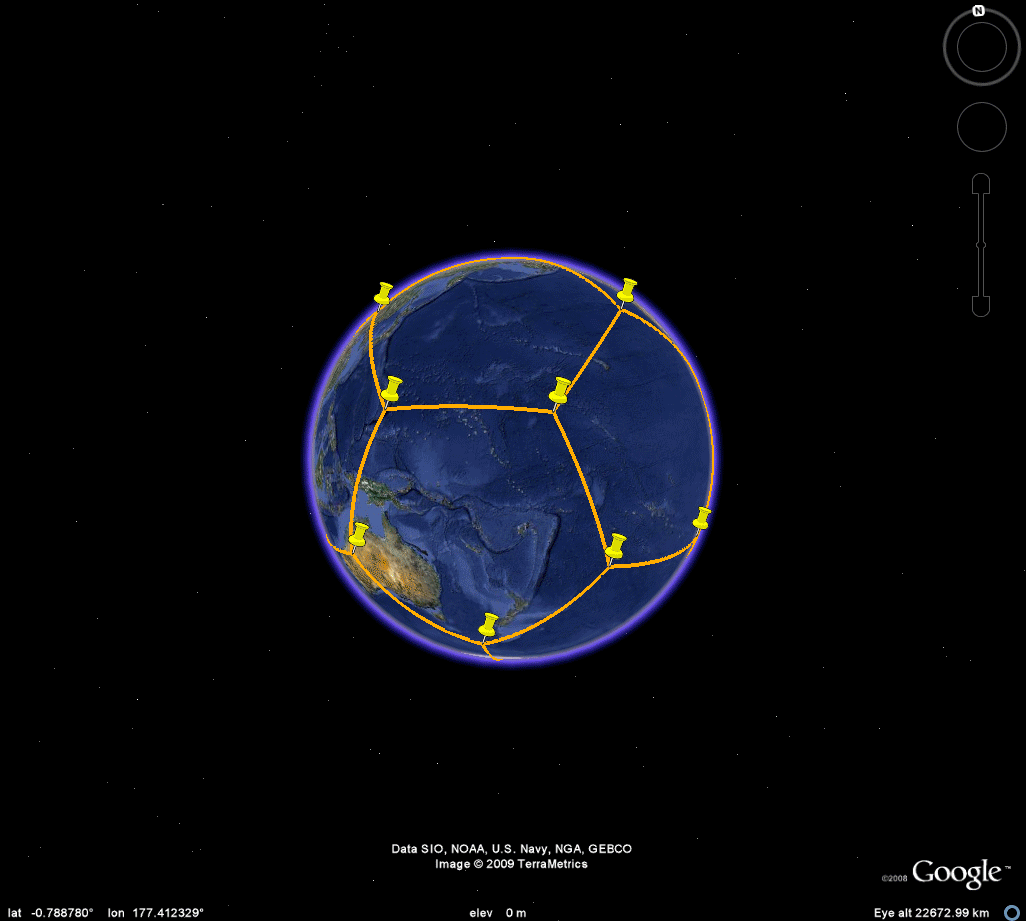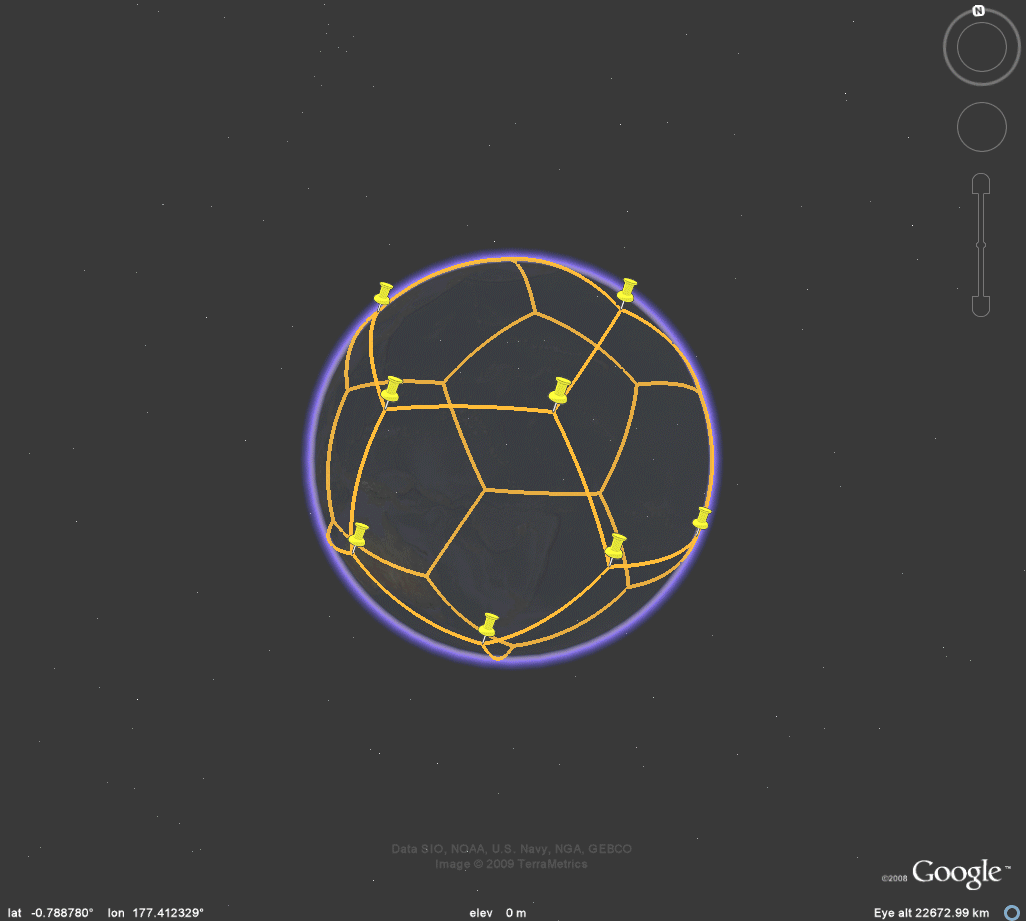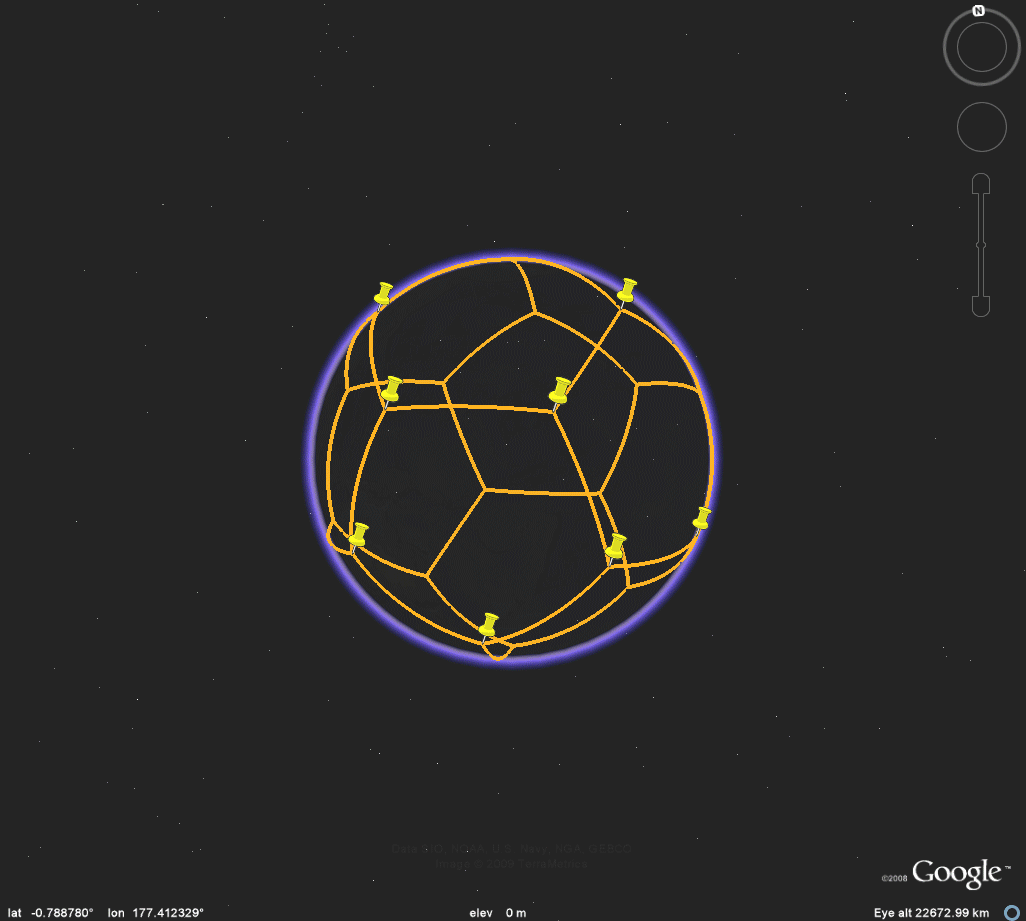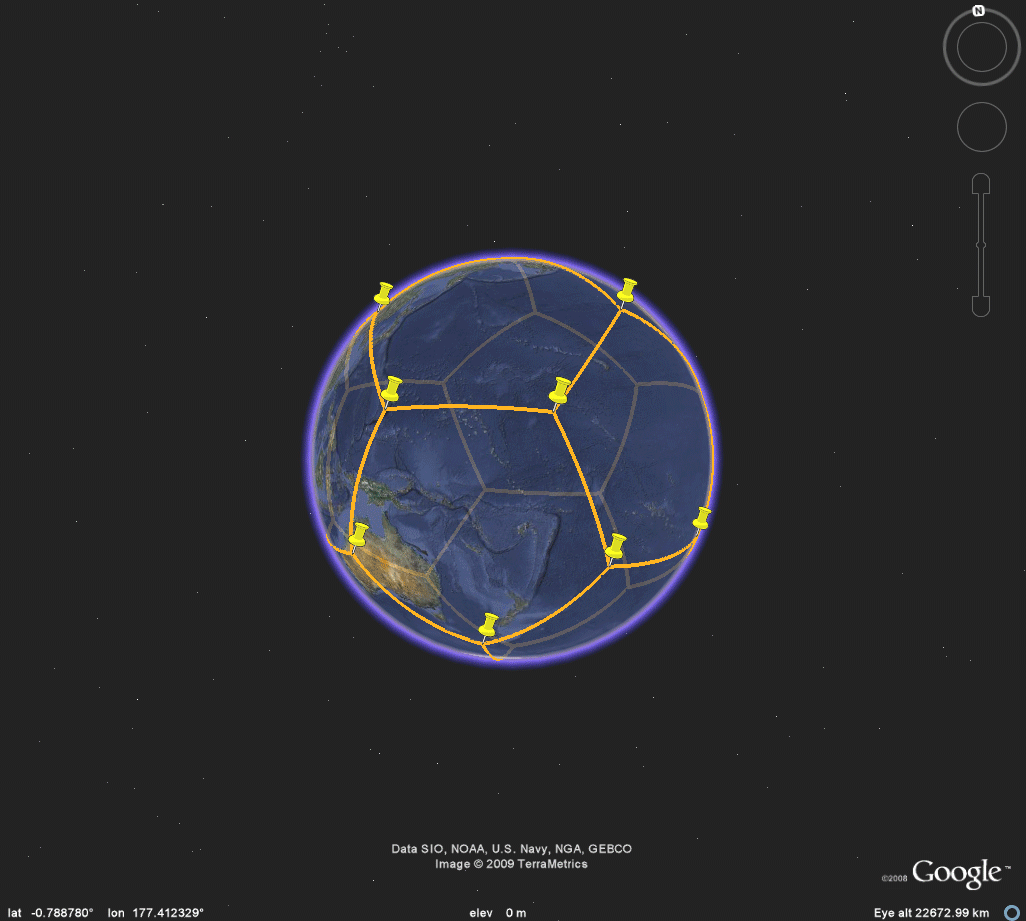 Figure 3d. Dodecahedron. |
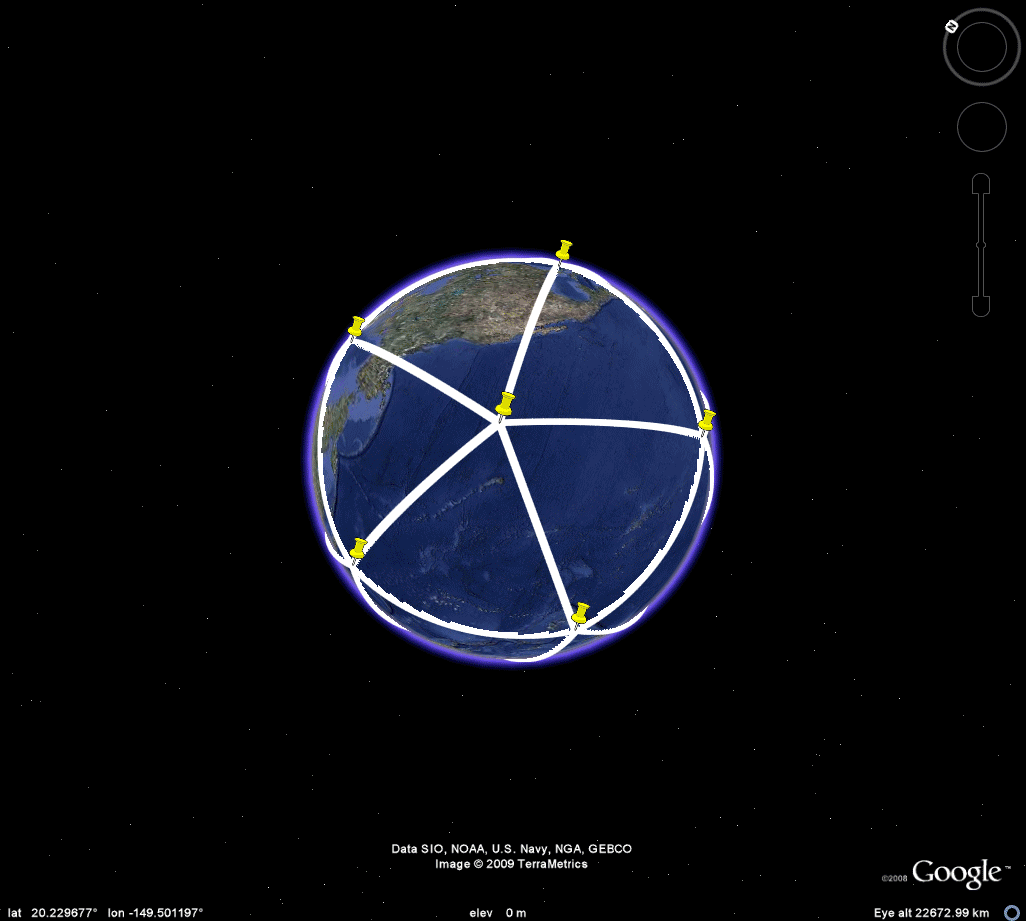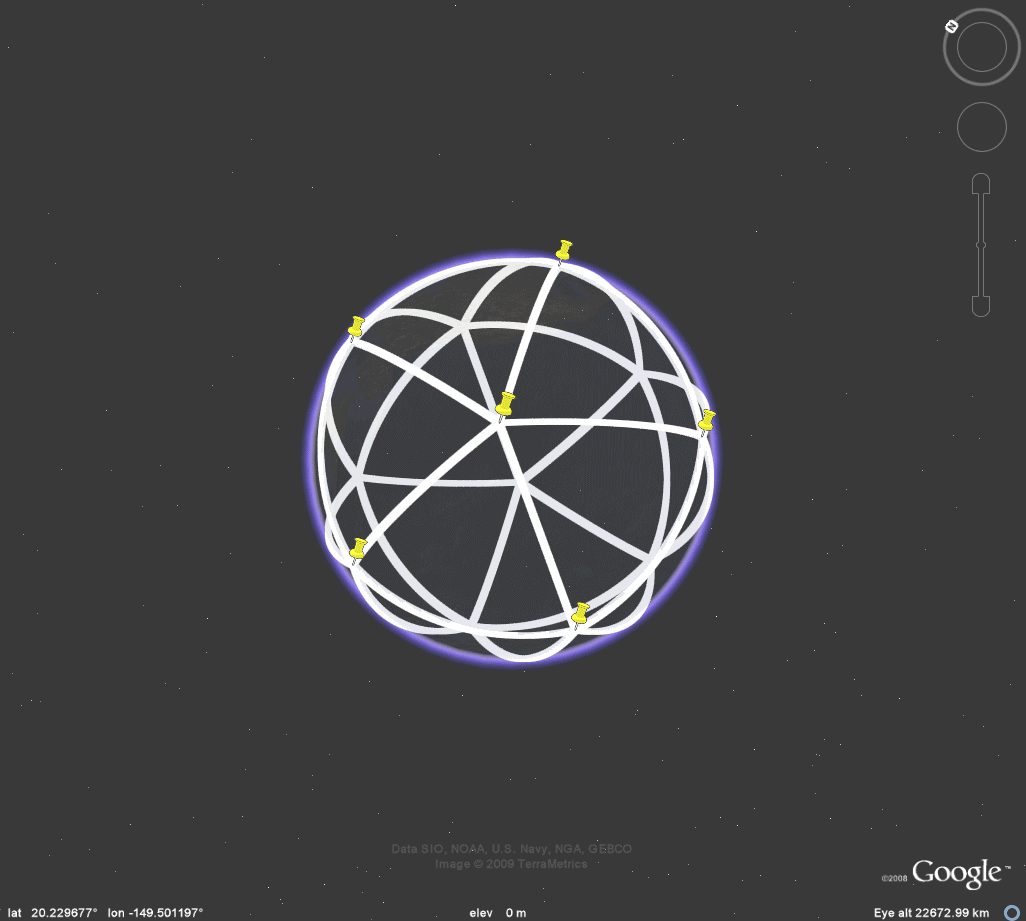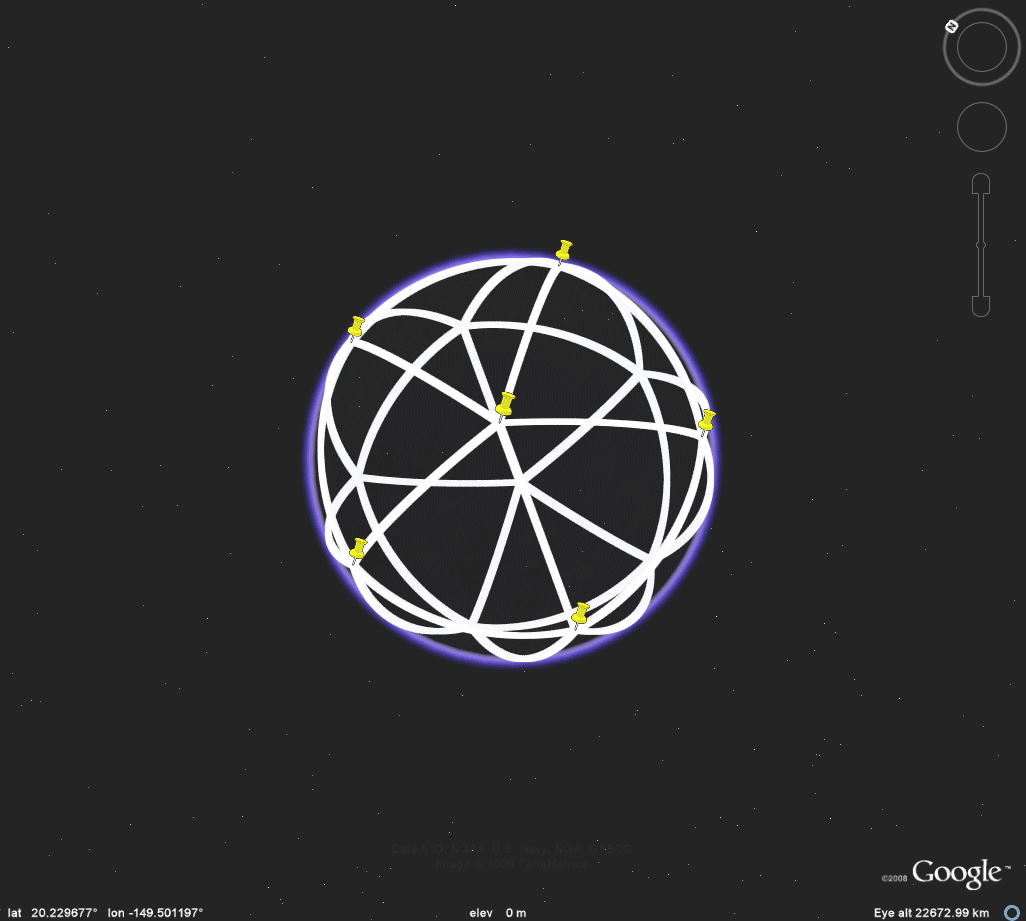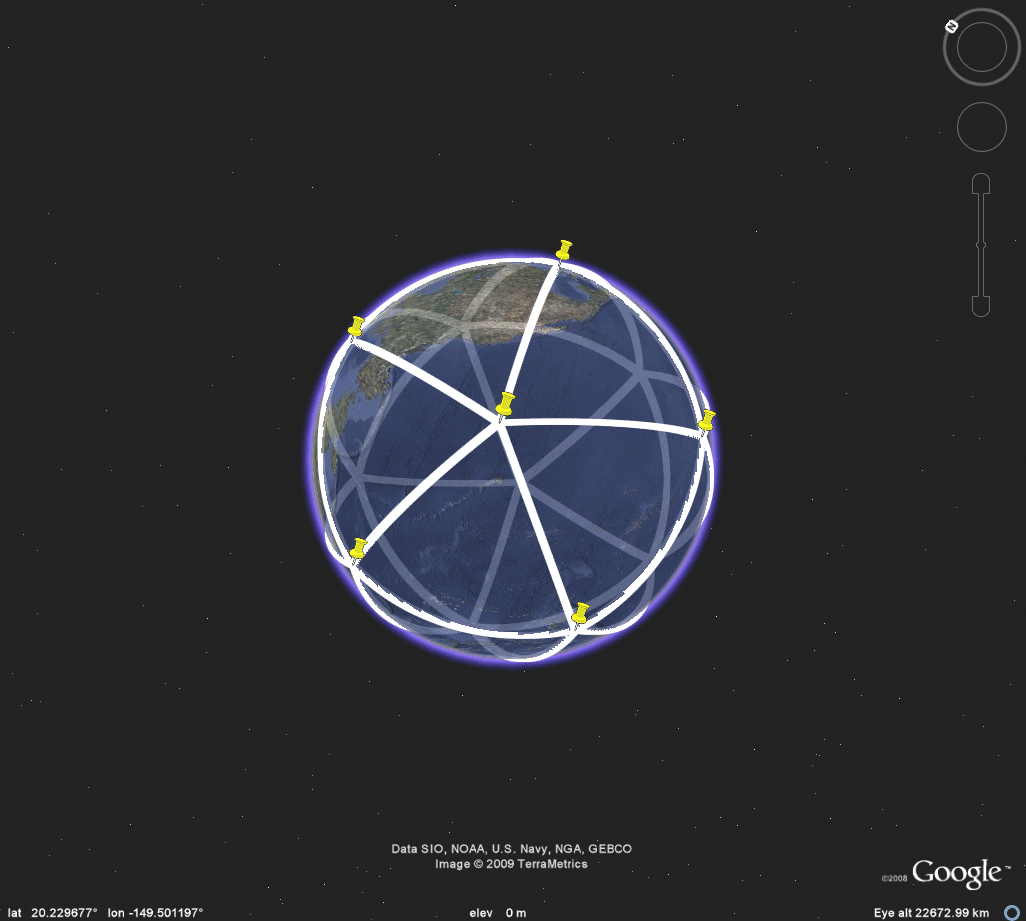 Figure 3e. Icosahedron. |
CUBE
 |
 |
OCTAHEDRON
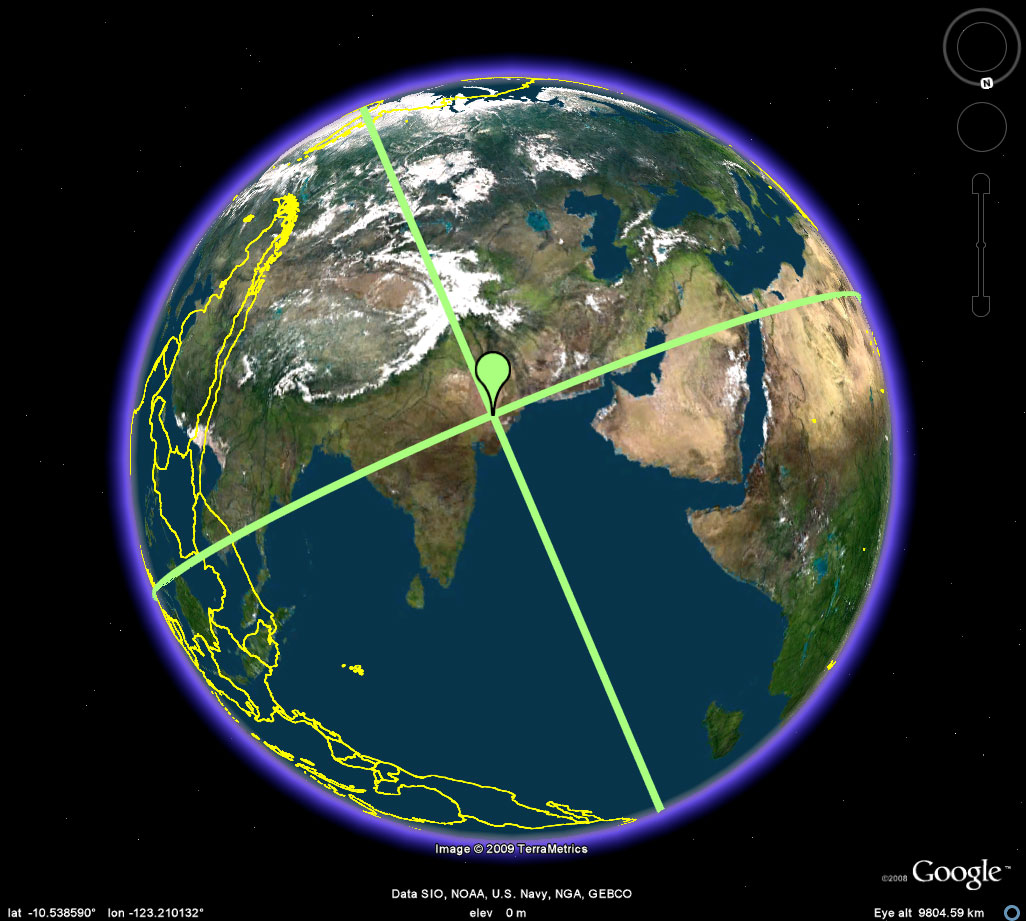 Figure 5a. Easter Island, on the outline map, marks its antipodal point in the Thar Desert in India. These antipodal points are antipodal vertices of the octahedron. The remaining four vertices all lie on a great circle in equatorial position between these two antipodal poles. |
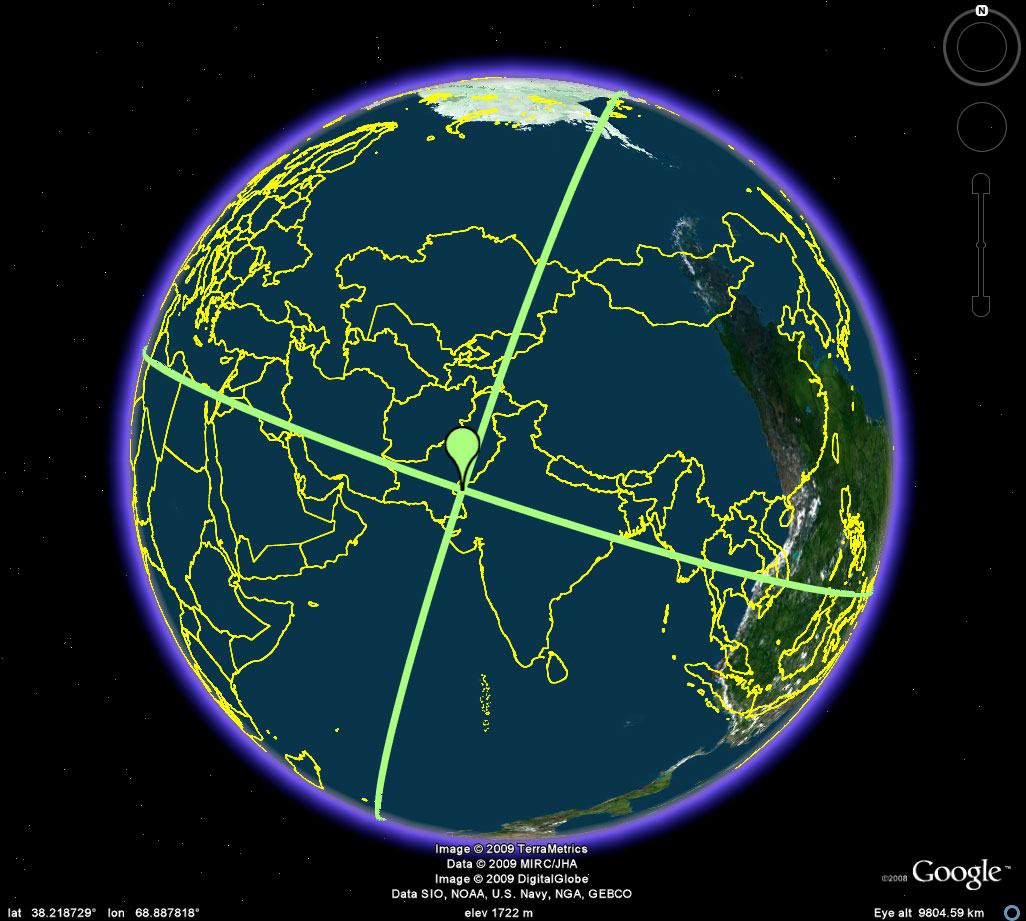 Figure 5b. Easter Island, on the antipodal skin map, marks its antipodal point on the outline map in the Thar Desert in India. These antipodal points are antipodal vertices of the octahedron. The remaining four vertices all lie on a great circle in equatorial position between these two antipodal poles. |
To visualize the remaining vertices in relation to each other requires the use of Terrae Antipodum because the full hemisphere cannot be viewed in Google Earth. The sequence in Figure 5 illustrates the process. It illustrates the "interval" strategy referred to in Figure 4 above.
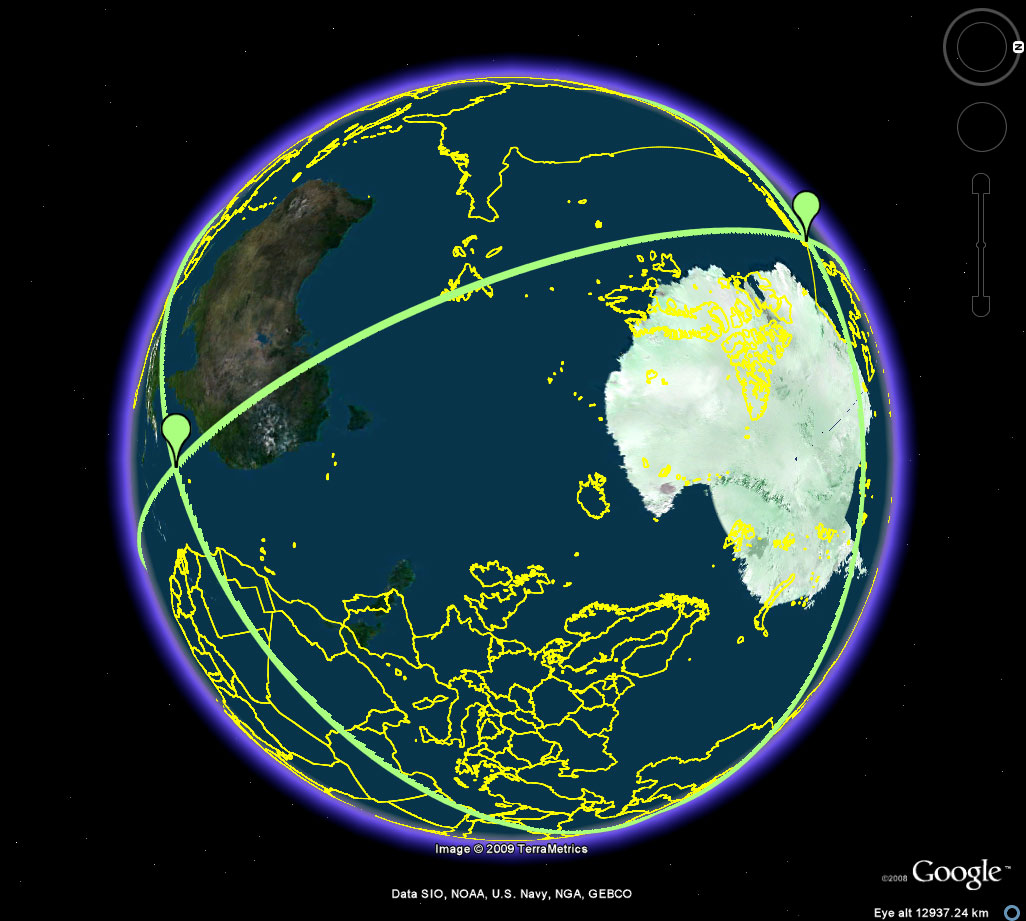 Figure 6a. The interval along the equatorial great circle (bisecting the antipodal poles of Easter Island and the Thar Desert. The yellow outline represents the Earth's continents. The colored skin is the antipodal lands map. The only candidate locations for vertex locations for the remaining four vertices are locations along the great circle where landmasses from both maps intersect. In this interval, it appears that there are no such candidates. A closer look might reveal otherwise; however, this scale is the scale in use here--there are some near misses in Australia. Thus, because there is no candidate in this interval, the octahedron cannot fulfull both of Barr's initial conditions. |
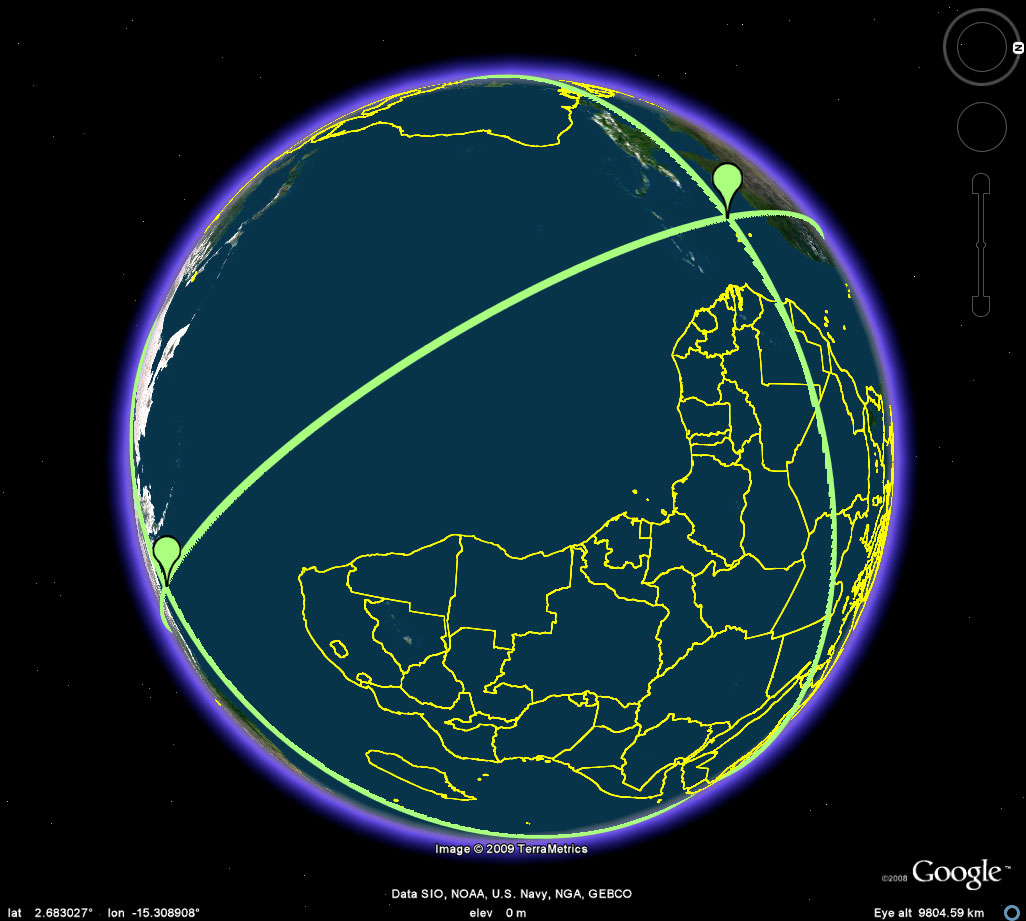 Figure 6.b. Again, another interval with no candidate points. |
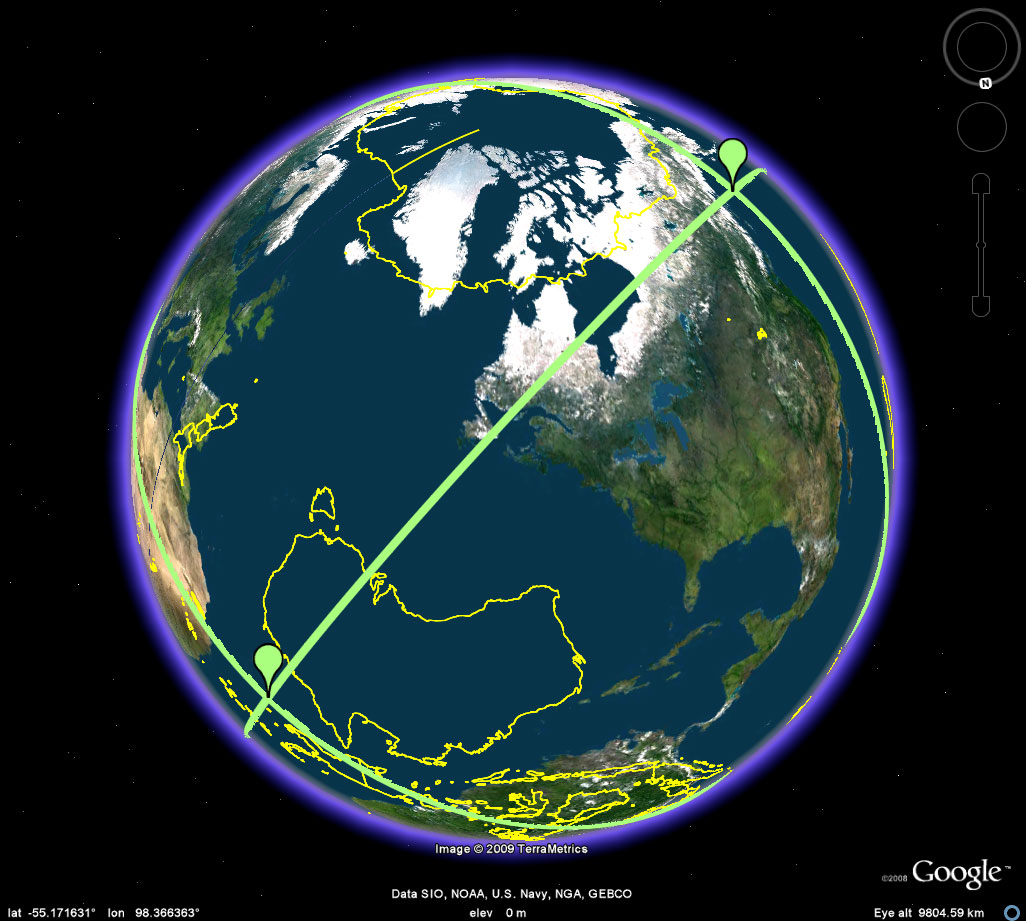 Figure 6c. Yet another interval along the great circle with no candidate points. |
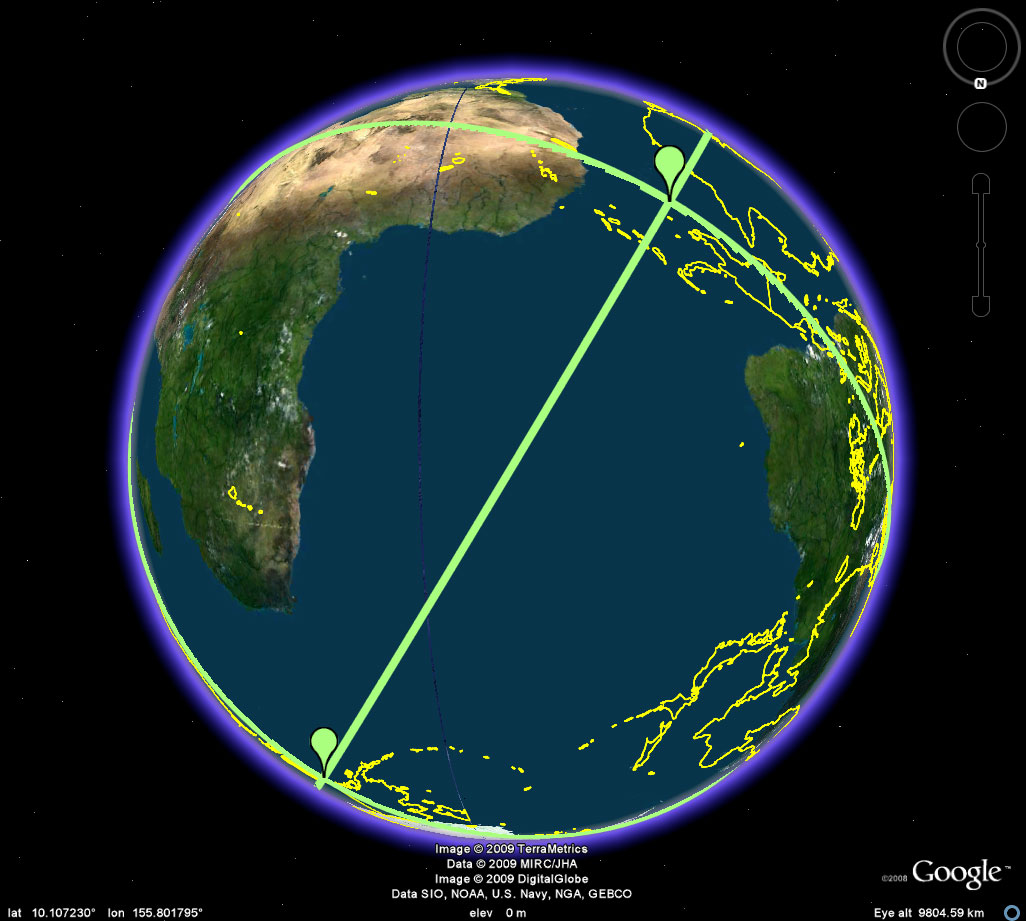 Figure 6d. The final interval also offers no candidate points. Thus, there is also no problem at the boundary points. |
 |
DODECAHEDRON
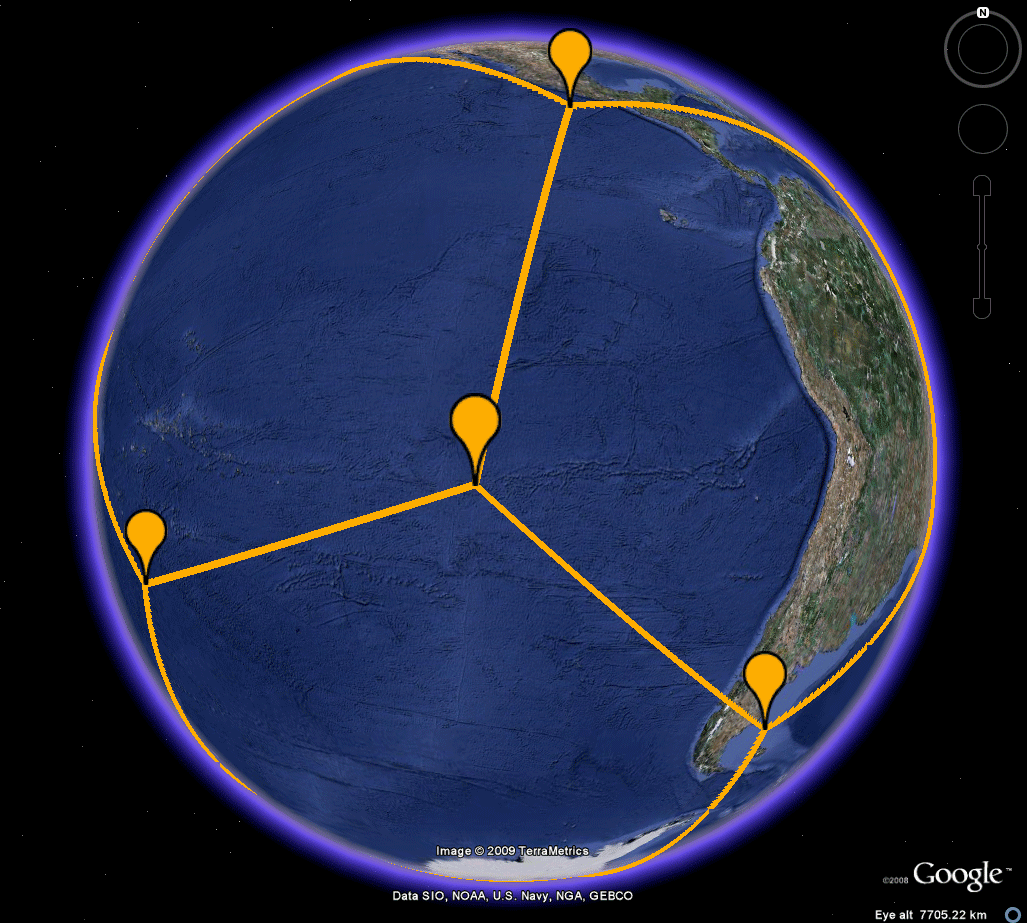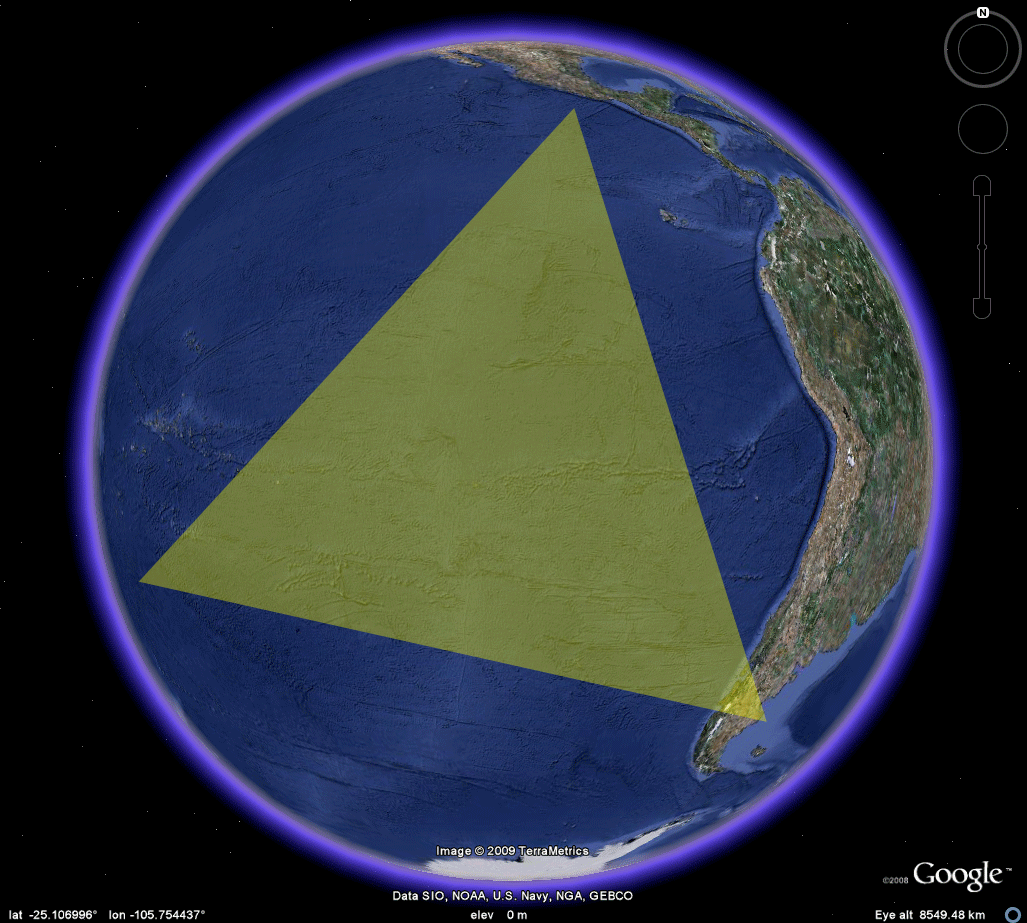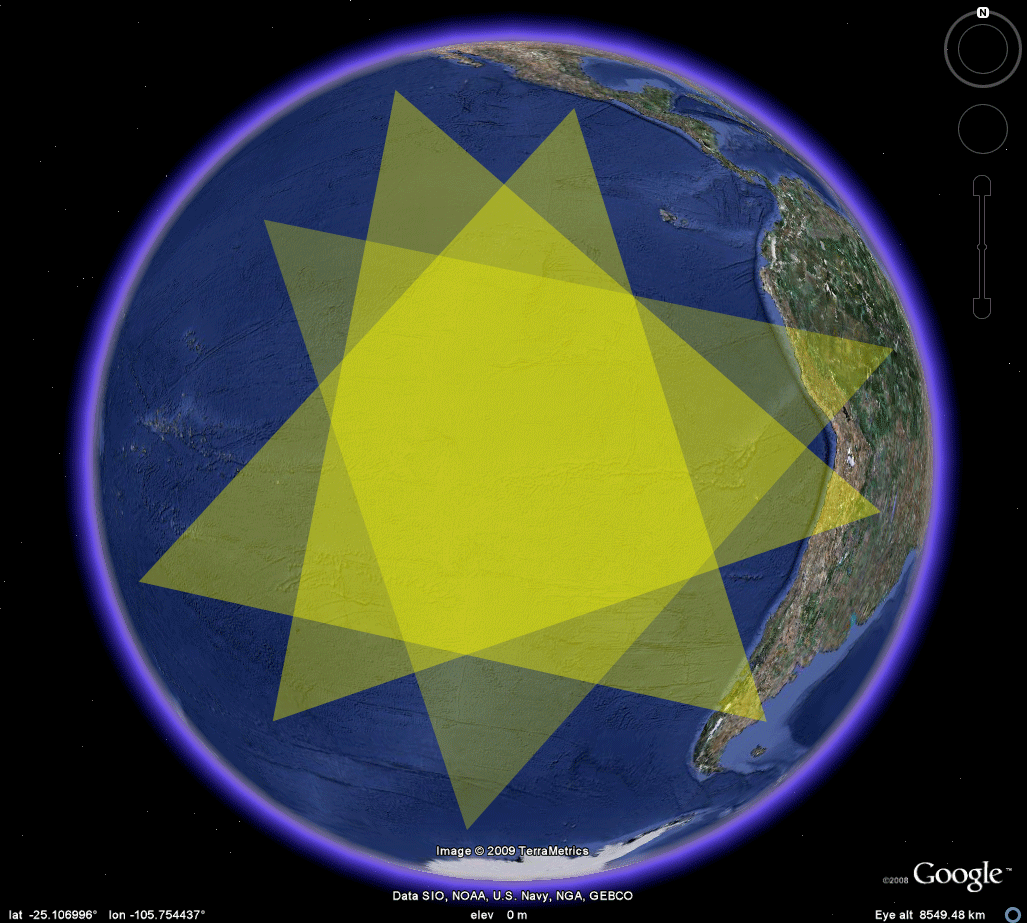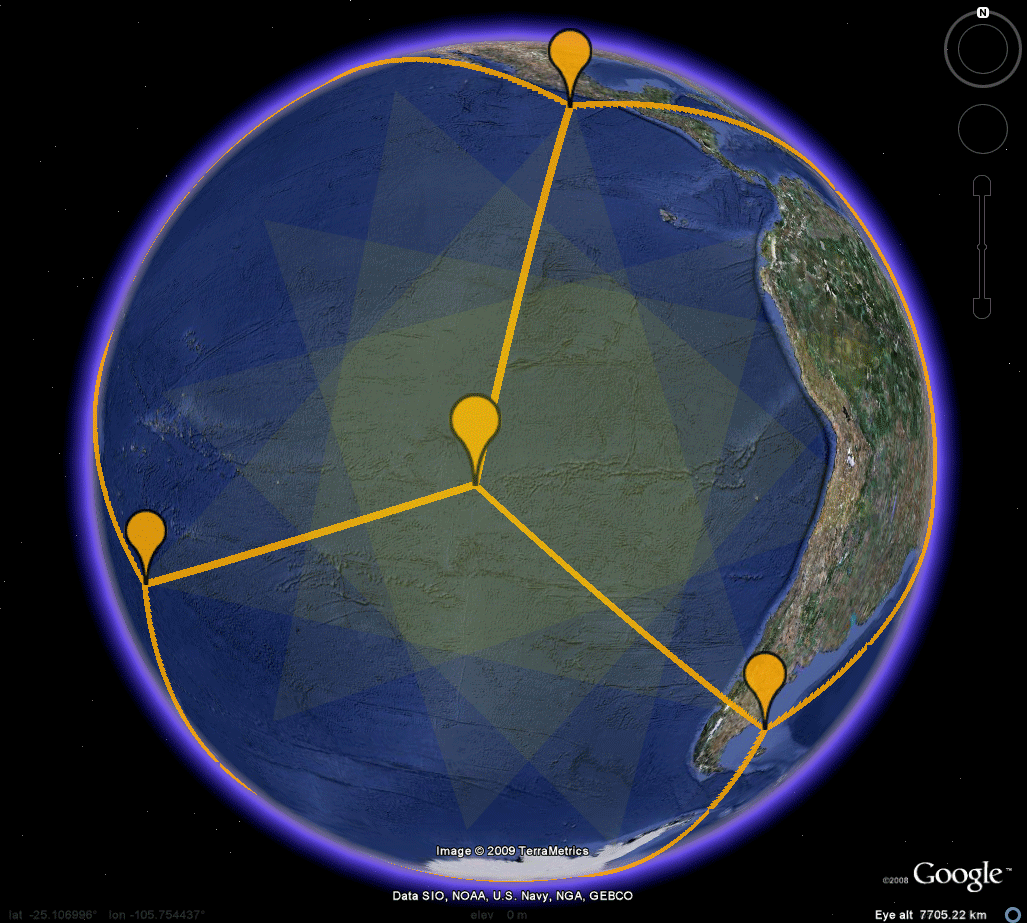 Figure 7a. The dodecahedron is embedded in the sphere, with one vertex at Easter Island. The yellow semi-transparent triangle represents three vertices adjacent to the vertex at Easter Island. All must be simultaneously placed on land. As the animation suggests, even if Antarctica is admitted as "land," such simultaneous placement is not possible. Thus, a dodecahedron could not have been selected. One might, however, wish to take a closer look lest some small islands serve as possible locations. The Google Earth .kmz file permits such a closer look. Depending on the scale chosen, simply chop the motion into suitable intervals from island to island to show that simultaneous placement of these three vertices on land is, or is not, possible. |
Figure
7b. In
the original text rough drawings and cardboard
cutouts were used for
analysis. The Google Earth capability
expands not only the
visualization level of the analysis but also its
precision.
|
ICOSAHEDRON
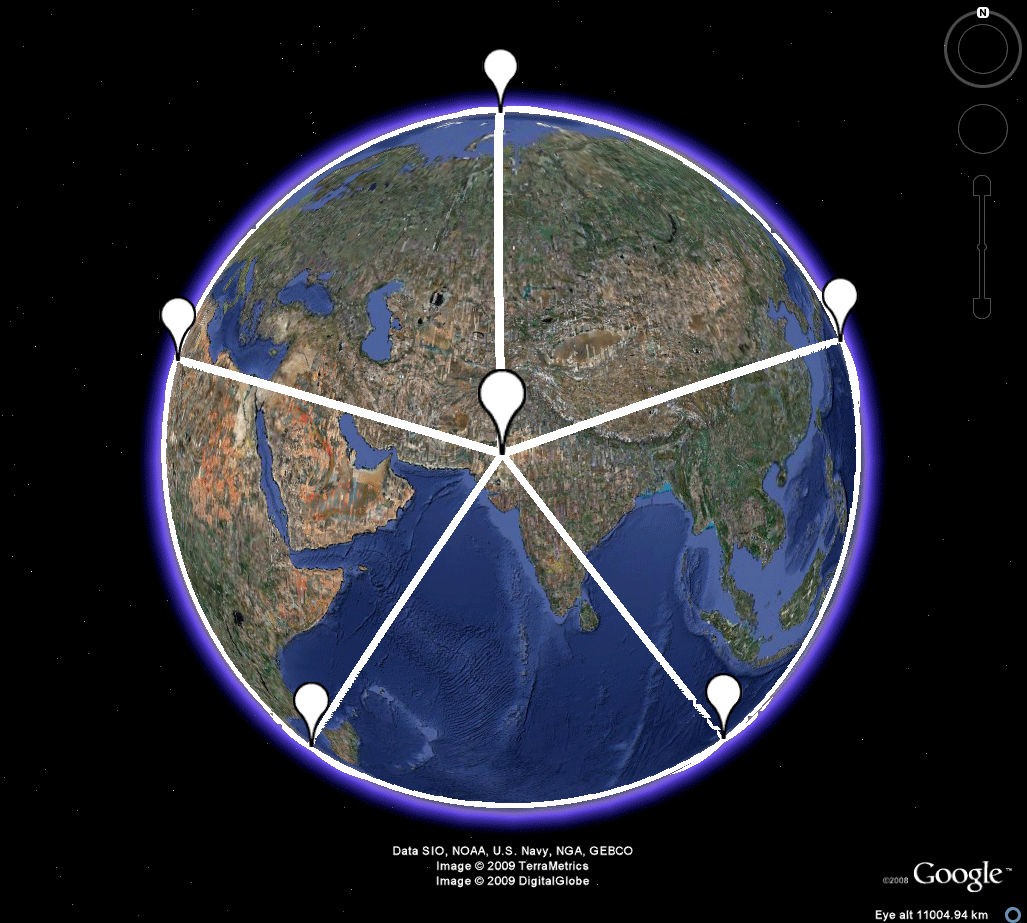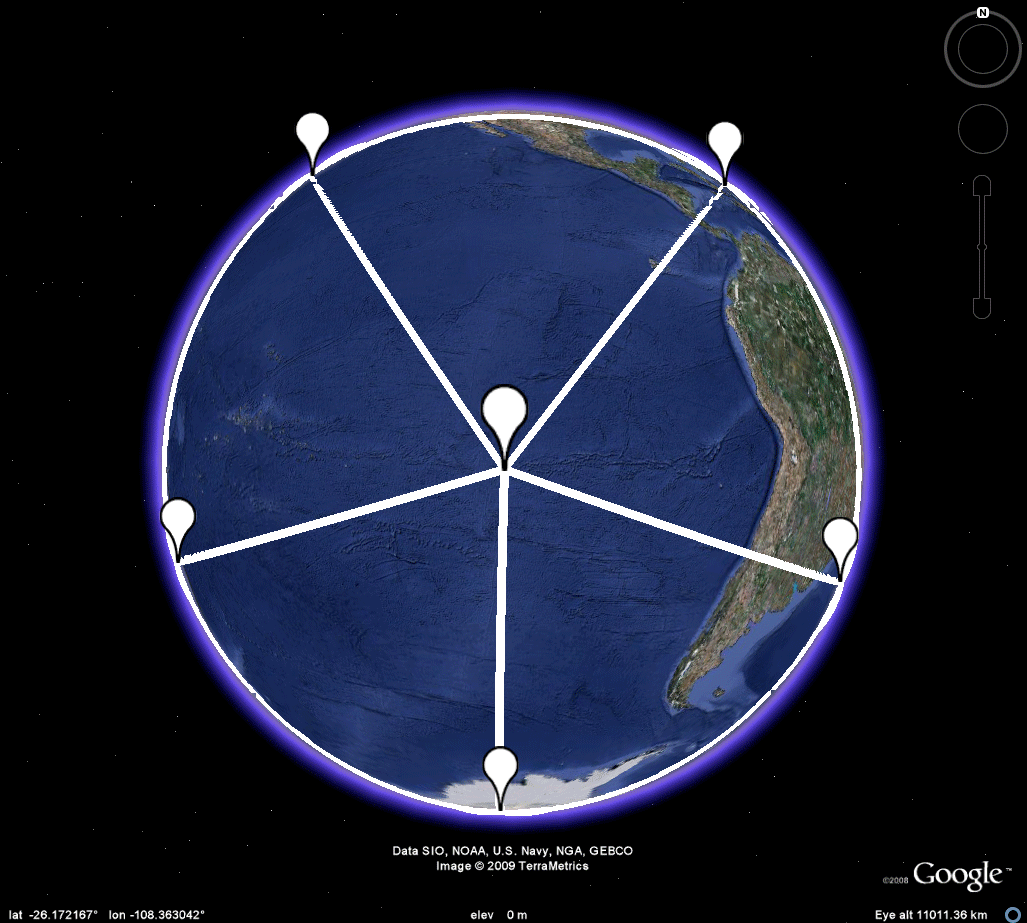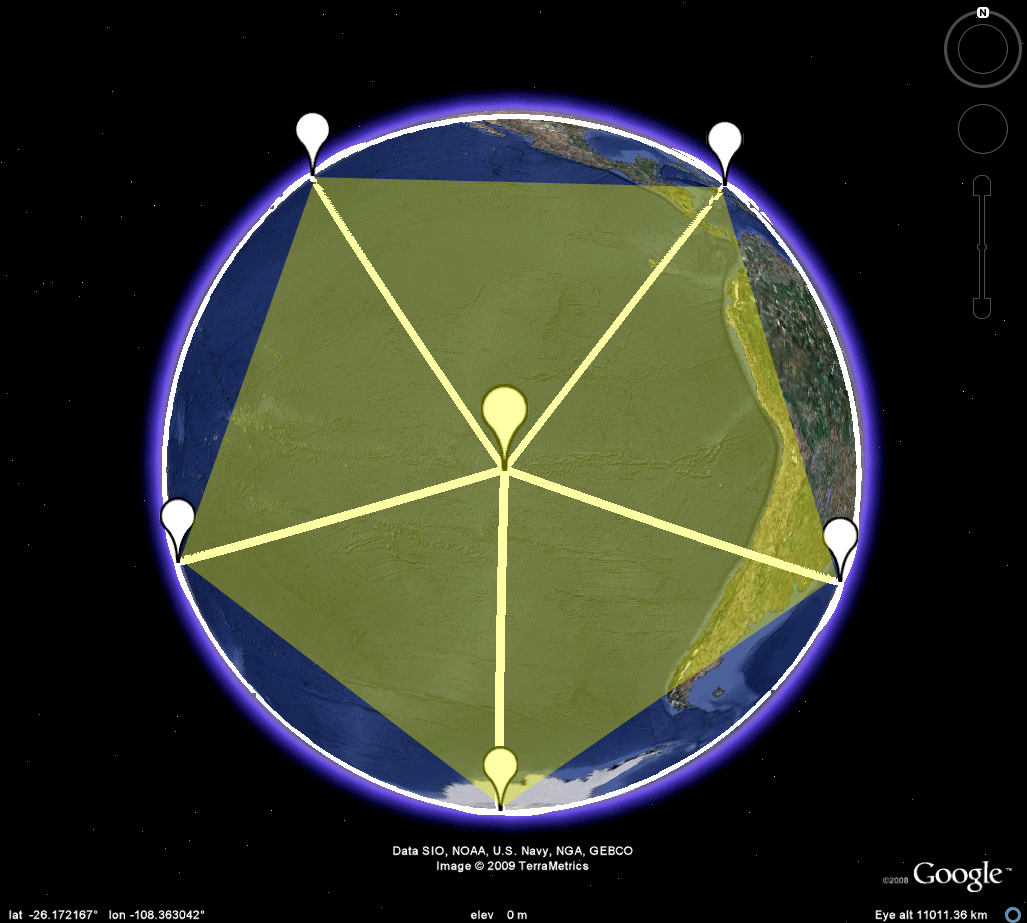 Figure 8a. Both Easter Island and its antipodal point in the Thar Desert serve as poles for the embedding of the icosahedron in the sphere. Each is surrounded by a set of five adjacent vertices, all of which must be land based. While one might imagine such a possibilty surrounding the Indian location, it is clearly not possible for the Easter Island set. The magnitude of the Pacific Ocean makes it impossible, at least at this scale and perhaps at all others! Take a further look in the .kmz file. |
Figure
8b. In
the
original
text rough drawings and cardboard cutouts were
used for
analysis. The Google Earth capability
expands not only the
visualization level of the analysis but also its
precision.
|
REFERENCES
- Appel,
Kenneth & Haken, Wolfgang, Every
Planar Map is Four-Colorable.
Providence, RI: American Mathematical Society, 1989.
- Archives
of American Art, Smithsonian Institution. "In
Celebration:
David Barr's 'Four Corners Project'." Film, July,
1985.
- Arlinghaus, Sandra L. Spatial Synthesis, Volume II, Book 4. Ann Arbor: Institute of Mathematical Geography, 2009.
- Arlinghaus,
Sandra
L. Antipodal graphs, Abstract #3792-92-404, Abstracts of the American
Mathematical Society, Vol. 3, No. 1, 1985.
http://www.ams.org/
- Arlinghaus, Sandra L. and Nystuen, John D. Mathematical Geography and Global Art: The Mathematics of David Barr's 'Four Corners Project. Institute of Mathematical Geography, Monograph #1, Ann Arbor, 1986.
- Arlinghaus, Sandra L. and Nystuen, John D. Mathematical Geography and Global Art: The Mathematics of David Barr's 'Four Corners Project. Institute of Mathematical Geography, Monograph #1, Revision, Forthcoming, Ann Arbor, 2009.
- Barr, David. Crossing Lines. Published by David Barr. Lithographs by Plucked Chicken Press with Will Petersen.
- Google EarthGrid Coordinates: Link to an online calculator.
- Tobler,
Waldo R. "World Map on a Möbius
Strip."
Surveying and Mapping,
XXI, 4,
1961, p. 486.
|
.

Solstice:
An
Electronic Journal of Geography and
Mathematics,
|
|
Congratulations to all Solstice contributors. |
Ann Arbor, MI 48104
734.975.0246
http://deepblue.lib.umich.edu/handle/2027.42/58219
image@imagenet.org